Bài Ôn tập chương I - ứng dụng đạo hàm để vẽ khảo sát và vẽ đồ thị của đạo hàm
Theo dõi 1.edu.vn trênA. Tổng quan kiến thức
I. Tính đơn điệu của hàm số
Quy tắc
- Tìm tập xác định.Tính $f'(x)$.
- Tìm các điểm tại đó để $f'(x)=0$ hoặc $f'(x)$ không xác định.
- Sắp xếp các điểm đó theo thứ tự tăng dần và lập bảng biến thiên.
- Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
II. Cực trị của hàm số
Quy tắc I
- Tìm tập xác định.Tính $f'(x)$.
- Tìm các điểm tại đó để $f'(x)=0$ hoặc $f'(x)$ không xác định.
- Lập bảng biến thiên.
- Từ bảng biến thiên, suy ra các điểm cực trị ( cực đại và cực tiểu ) của hàm số.
Quy tắc II
- Tìm tập xác định.Tính $f'(x)$.
- Giải phương trình $f'(x)=0$ và kí hiệu $x_{i} ( i =0,1,2,... )$ là các nghiệm của nó.
- Tính $f''(x)$ và $f''(x_{i})$.
- Dựa vào dấu của $f''(x_{i})$ suy ra tính chất cực trị của điểm $x_{i}$.
II. Cách tìm GTLN ( max ) và GTNN ( min ) của hàm số trên một đoạn
Quy tắc
- Tìm các điểm $x_{1},x_{2},..,x_{n}$ trên khoảng (a;b), tại đó $f'(x)=0$ hoặc không xác định.
- Tính $f(a),f(x_{1}),f(x_{2}),..,f(x_{n}),f(b)$.
- Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
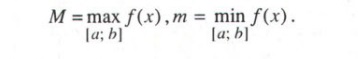
Ví dụ:
Từ bảng biến thiên sau:
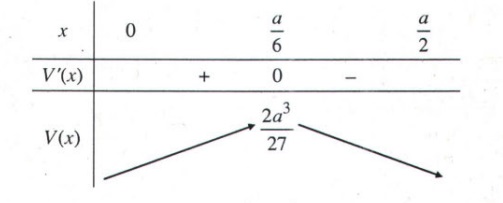
==> Kết luận: $max V(x)=\frac{2a^{3}}{27}$ với $x\in (0,\frac{a}{2})$.
IV. Đường tiệm cận
1. Đường tiệm cận ngang
Cho hàm số $y=f(x)$ xác định trên một khoảng vô hạn $(-\infty ;+\infty )$.
Nếu $\lim_{x \to \pm \infty }=y_{0} => y=y_{0}$ là đường tiệm cận ngang .
Ví dụ:
Hàm số $f(x)=\frac{1}{\sqrt{x}}+1$ xác định trên khoảng $(0;+\infty )$.
Ta có: $\lim_{x \to +\infty }f(x)=\lim_{x \to +\infty }(\frac{1}{\sqrt{x}}+1)=1$
=> $y=1$ là tiệm cận ngang của hàm số đã cho.
2. Đường tiệm cận đứng
Cho hàm số $y=f(x)$ , nếu thỏa mãn một trong số các điều kiện sau:
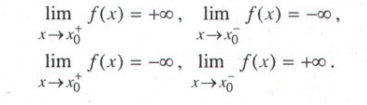
=> $x=x_{0}$ là tiệm cận đứng của hàm số $y=f(x)$.
V. Khảo sát và vẽ đồ thị hàm số
1. Sơ đồ khảo sát đồ thị có 3 bước:
- Bước 1: Tập xác định.
- Bước 2: Sự biến thiên.
- Bước 3: Đồ thị.
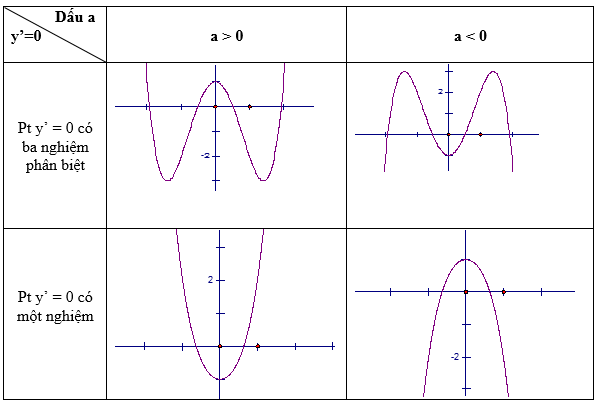
2. Một số dạng đồ thị với hàm số bậc ba $y=ax^{3}+bx^{2}+cx+d (a\neq 0)$
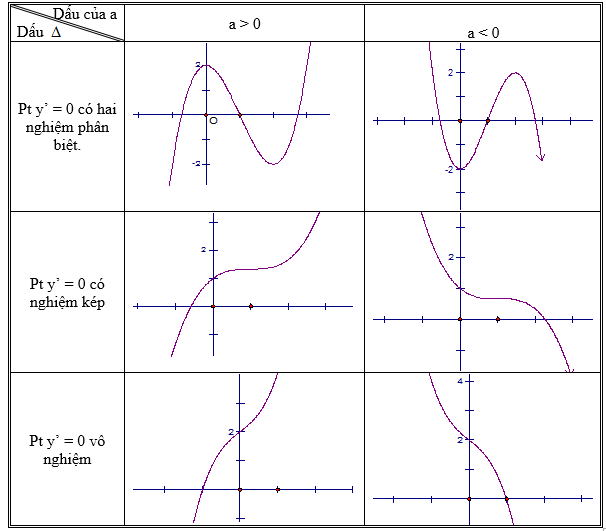
3. Một số dạng đồ thị với hàm số bậc bốn $y=ax^{4}+bx^{2}+c (a\neq 0)$
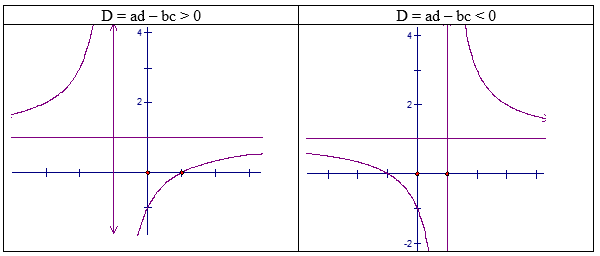
4. Hàm số $y=\frac{ax+b}{cx+d} (c\neq 0,ad-bc\neq 0)$
B. Bài tập & Lời giải
Câu 1:Trang 45 - sgk giải tích 12
Phát biểu các điều kiện đồng biến và nghịch biến của hàm số.
Tìm các khoảng đơn điệu của hàm số:
$y=-x^{3}+2x^{2}-x-7$
$y=\frac{x-5}{1-x}$
Xem lời giải
Câu 2:Trang 45 - sgk giải tích 12
Nêu cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm.
Tìm các cực trị của hàm số: $y=x^{4}-2x^{2}+2$
Xem lời giải
Câu 3: Trang 45 - sgk giải tích 12
Nêu cách tìm ra tiệm cận ngang và tiệm cận dứng của đồ thị hàm số.
Áp dụng để tìm các tiệm cận của đồ thị hàm số: $y=\frac{2x+3}{2-x}$
Xem lời giải
Câu 4: Trang 45 - sgk giải tích 12
Nhắc lại sơ đồ khảo sát sự biến thiên và vẽ đồ thị của hàm số.
Xem lời giải
Câu 5: Trang 45 - sgk giải tích 12
Cho hàm số $y = 2x^{2} + 2mx + m - 1$ có đồ thị là ($C_{m}$), m là tham số.
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m = 1$.
b) Xác định m để hàm số:
i) Đồng biến trên khoảng $(-1; +∞)$.
ii) Có cực trị trên khoảng $(-1; +∞)$.
c) Chứng minh rằng ($C_{m}$) luôn cắt trục hoành tại hai điểm phân biệt với mọi m.
Xem lời giải
Câu 6: Trang 45 - sgk giải tích 12
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: $f(x) = -x^{3} + 3x^{2} + 9x + 2$
b) Giải phương trình $f'(x - 1) > 0$.
c) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ $x_{0}$, biết rằng $f'(x_{0}) = -6$.
Xem lời giải
Câu 7: Trang 45 - sgk giải tích 12
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = x^{3} + 3x^{2} + 1$
b) Dựa vào đồ thị (C), biện luận số nghiệm phương trình sau theo m: $x^{3} + 3x^{2} + 1 = \frac{m}{2}$
c) Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị (C).
Xem lời giải
Câu 8: Trang 46 - sgk giải tích 12
Cho hàm số: $f(x) = x^{3} - 3mx^{2} + 3(2m - 1)x + 1$ (m là tham số).
a) Xác định m để hàm số đồng biến trên tập xác định.
b) Với giá trị nào của tham số m thì hàm số có một cực đại và một cực tiểu?
c) Xác định m để $f"(x) > 6x$.
Xem lời giải
Câu 9: Trang 46 - sgk giải tích 12
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: $\frac{1}{2}x^{4}-3x^{2}+\frac{3}{2}$
b) Viết phương tình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là nghiệm của phương trình $f"(x) = 0$.
c) Biện luận theo tham số m số nghiệm của phương trình: $x^{4} - 6x^{2} + 3 = m$.
Xem lời giải
Câu 10: Trang 46 - sgk giải tích 12
Cho hàm số $y = -x^{4} + 2mx^{2} - 2m + 1$ (m tham số) có đồ thị là ($C_{m}$).
a) Biện luận theo m số cực trị của hàm số.
d) Với giá trị nào của m thì ($C_{m}$) cắt trục hoành?
c) Xác định để ($C_{m}$) có cực đại, cực tiểu.
Xem lời giải
Câu 11: Trang 46 - sgk giải tích 12
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số $y=\frac{x+3}{x+1}$
b) Chứng minh rằng với mọi giá trị của đường thẳng $y = 2x + m$ luôn cắt (C) tại hai điểm phân biệt M và N.
c) Xác định m sao cho độ dài MN nhỏ nhất.
Xem lời giải
Câu 12: Trang 46 - sgk giải tích 12
Cho hàm số $f(x)=\frac{1}{3}x^{3}-\frac{1}{2}x^{2}-4x+6$
a) Giải phương trình $f'(sin x) = 0$.
b) Giải phương trình $f"(cos x) = 0$.
c) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ là nghiệm của phương trình $f"(x) = 0$.