Câu hỏi và bài tập trắc nghiệm toán 12 bài Ôn tập chương 4 - số phức
Theo dõi 1.edu.vn trênCâu 1: Cho số phức $z$ thỏa mãn $|z + 2 - i| + |z - 4 -7i| = 6\sqrt{2}$ Gọi $M, m$ lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức $P = |z - 1 + i|$. Giá trị của tổng $S = M + m$ là:
- A. $S= \frac{2\sqrt{29} = 3\sqrt{2}}{2}$
- B. $S= \sqrt{13} + \sqrt{73}$
- C. $S= 5\sqrt{2} + \sqrt{73}$
-
D. $S= \frac{2\sqrt{73} + 5\sqrt{2}}{2}$
Câu 2: Trong mặt phẳng tọa độ $Oxy$, gọi $H$ là phần mặt phẳng chứa các điểm biểu diễn của các số phức z thỏa mãn $\frac{z}{40}$ và $\frac{40}{\bar{z}}$ có phần thực và ảo đều thuộc [0; 1] . Tính diện tích của $H$
- A. 1600.
- B. 400π.
- C. 50(3 - π).
-
D. 1200- 200π .
Câu 3: Giả sử $M (z) $ là điểm trên mặt phẳng phức biểu diễn số phức $z$. Tập hợp các điểm $M (z)$ thỏa mãn điều kiện $| z- 1+ i|= 2$ là một đường tròn:
- A. Có tâm (- 1; -1) và bán kính là 2
- B. Có tâm (1; -1) và bán kính là $\sqrt{2}$
- C. Có tâm (- 1; 1) và bán kính là 2
-
D. Có tâm (1; -1) và bán kính là 2
Câu 4: Cho các số phức $z$ thỏa mãn $|z- i| = |z- 1+ 2i|$. Tập hợp các điểm biểu diễn các số phức $w= (2- i)z + 1$ trên các mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó?
- A. $-x+ 7y+ 9= 0$
- B. $x+ 7y- 9= 0$
-
C. $x+ 7y+ 9= 0$
- D. $x- 7y+ 9= 0$
Câu 5: Tập hợp các điểm biểu diễn số phức $z$ thỏa mãn $|z- 2- i| = | \bar{z} + 2i|$ là đường thẳng nào sau đây?
- A. $4x- 2y+ 1= 0$
- B. $4x- 6y- 1= 0$
- C. $4x+ 2y- 1= 0$
-
D. $4x - 2y- 1= 0$
Câu 6: Cho số phức $z = a + bi, (a ≥ 0; b ≥ 0; a, b ∈ R)$. Đặt $f(x) = ax^{2} + bx - 2$. Biết:
$f(-1) \leq 0; f(\frac{1}{4}) \leq -\frac{5}{4}$
Tính giá trị lớn nhất của |z| .
-
Amax$|z|$ = $2\sqrt{5}$
- B. max$|z|$ = $3\sqrt{2}$
- C. max$|z|$ = 5
- D. max$|z$| = $2\sqrt{6}$
Câu 7: Trong mặt phẳng tọa độ, miền trong hình chữ nhật ABCD (kể cả các cạnh $AB, BC, CD, DA$ ) trong hình vẽ biểu diễn cho các số phức $z$. Chọn khẳng định đúng.
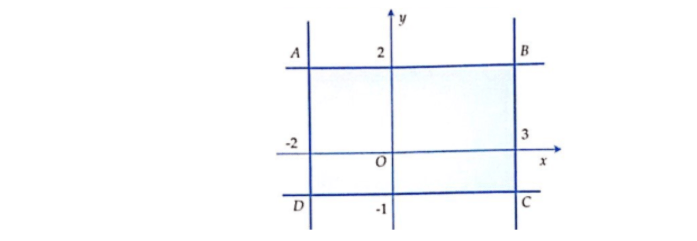
- A. Phần ảo của số phức $z- \bar{z}$ lớn hơn 4
- B. Phần thực của $z + \bar{z}$ nhỏ hơn 4
- C. Giá trị nhỏ nhất của $|z|$ bằng 1
-
D. Giá trị lớn nhất của $|z|$ bằng $\sqrt{13}$
Câu 8: Cho số phức z thỏa mãn $|z - 1 + 3i| + |z + 2 - i| = 8$. Tìm giá trị lớn nhất, giá trị nhỏ nhất của $P = |2z + 1 + 2i|.$
-
A. max$P$ = 8; min$P$ = $\sqrt{39}$
- B.max$P$ = 10; min$P$ = $\sqrt{39}$
- C. max$P$ = 8; min$P$= 6.
- D. max$P$ = 10; min$P$ = 6
Câu 9: Cho hai số phức $z_{1}, z_{2}$ thỏa mãn $|z1| = 2, |z2| = \sqrt{3}$ và nếu gọi $ M, N$ lần lượt là điểm biểu diễn cho các số phức $z_{1}, z_{2}$ thì:
- A. $P = \sqrt{5}. $
-
B. $P = 4\sqrt{7}$
- C. $P = 3\sqrt{3} $
- D. $P = 5\sqrt{2}$
Câu 10: Cho số phức z thoả mãn $|z - 3 - 4i| = \sqrt{5}$. Gọi $M$ và $m$ là giá trị lớn nhất và giá trị nhỉ nhất của biểu thức $P = |z + 2|^{2} - |z - i|^{2}$. Tính module số phức $w = M + mi$
- A. $|w| = 2\sqrt{314}$
- B. $|w| = 2\sqrt{137}$
-
C. $|w| = 2\sqrt{1258}$
- D. $|w| = 2\sqrt{309}$
Câu 11: Trong mặt phẳng tọa độ, hình tròn tô đậm như hình vẽ dưới đây là tập hợp điểm biểu diễn số phức. Hỏi số phức $z$ thỏa mãn bất đẳng thức nào sau đây?
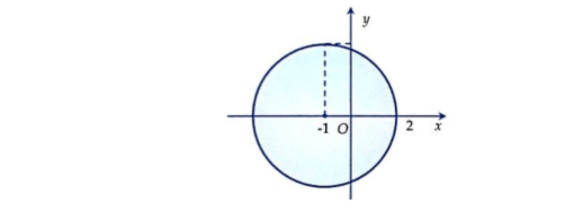
- A. $|z - 1| \leq 3$
- B. $|z - i| \leq 3$
-
C. $|z + 1| \leq 3$
- D. $|z + i| \leq 3$
Câu 12: Cho số phức z thoả mãn:
Giá trị lớn nhất của biểu thức $P = |z - 5 - 2i|$ bằng
-
A. $\sqrt{2} + 5\sqrt{3}$
-
B. $\sqrt{2}+ 3\sqrt{5}$
- C. $\sqrt{5}+ 2\sqrt{3} $
- D. $\sqrt{5}+ 3\sqrt{2}$
Câu 13: Biết các số phức $z$ có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là hình vuông tô đậm như hình vẽ bên. Tập hợp các điểm biểu diễn số phức $z + 2$ là:
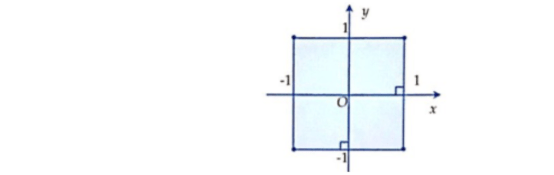
- A. Hình vuông có tâm (0; 0) và có 1 đỉnh là (2; 2)
- B. Hình vuông có tâm (0; 2) và có 1 đỉnh là (1; 3)
-
C. Hình vuông có tâm (2; 0) và có 1 đỉnh là (3; 1)
- D. Hình vuông có tâm (0; -2) và có 1 đỉnh là (-1; 1)
Câu 14: Gọi $z_{1}, z_{2}$ là hai nghiệm của phương trình $z^{2} - 2z + 6 = 0$. Trong đó $z_{1}$ có phần ảo âm. Giá trị biểu thức $M = |z_{1}| + |3z_{1}, z_{2}| $ là:
- A. $ 2 \pm i\sqrt{2}$ hoặc
$ -2 \pm 2i\sqrt{2}$
- B. $ 2 \pm i\sqrt{2}$ hoặc $ 1 \pm 2i\sqrt{2}$
- C. $ 1 \pm 2i\sqrt{2}$ hoặc $ -2 \pm 2i\sqrt{2}$
- D. $ -1 \pm 2i\sqrt{2}$ hoặc $ -2 \pm 2i\sqrt{2}$
Câu 15: Gọi $z_{1}, z_{2}$ là hai nghiệm của phương trình $z^{2} + 2z + 8 = 0$, trong đó $z_{1}$ có phần ảo dương. Giá trị của số phức $w= (2z_{1}+ z_{1}).\bar{z_{1}}$ là:
- A. 12 + 6$i $
- B. 10
-
C. 8
- D. 12 - 6$i$
Câu 16: Cho số phức $z$ có số phức liên hợp $\bar{z}$ thỏa mãn $| z^{2} - (\bar{z})^{2}|$ = 4. Tập hợp các điểm biểu diễn số phức $z$ trên mặt phẳng tọa độ là:
- A. Đường cong $y= \frac{1}{x}$
- B. Đường thẳng $y= x$
- C. Hai đường thẳng $y= x$ và $y= -x$
-
D. Hai đường cong $y= \frac{1}{x}$ và $y= -\frac{1}{x}$
Câu 17: Cho số phức $z$ thỏa mãn $|z|$ = 1. Tìm giá trị lớn nhất và nhỏ nhất của $M$ với M= $|z^{2} + z+ 1| + |z^{3} + 1|$
-
A. $Mmax = 5; Mmin= 1$
- B. $Mmax = 5; Mmin= 2$
- C. $Mmax = 4; Mmin= 1$
- D. $Mmax = 4; Mmin= 2$
Câu 18: Cho số phức $z$ thỏa mãn $|z| \geq 2$. Tìm giá trị của Max$P$.Min$P$ với $P = |\frac{z+i}{z}|$
-
A. $\frac{3}{4}$
- B. 1
- C. 2
- D. $\frac{2}{3}$
Câu 19: Cho số phức $z$ thỏa mãn điều kiện $|z^{2} + 4|= 2|z|$$. Khẳng định nào sau đây là đúng?
- A. $\frac{\sqrt{3}-1}{6} \leq |z| \leq \frac{\sqrt{3}+1}{6}$
- B. $\sqrt{5} - 1 \leq |z| \leq \sqrt{5} + 1$
- C. $\sqrt{6} - 1 \leq |z| \leq \sqrt{6} + 1$
-
D. $\frac{\sqrt{2}-1}{3} \leq |z| \leq \frac{\sqrt{2}+1}{3}$
Câu 20: Biết số phức $z$ thỏa mãn đồng thời hai điều kiện $|z- 3- 4i| = \sqrt{5}$ và biểu thức $M = |z+2|^{2} - |z- i|^{2}$ đạt giá trị lớn nhất. Tính $|z + i|$?
-
A. $|z + i|$ = $\sqrt{61}$
- B. $|z + i|$ = 3$\sqrt{5}$
- C. $|z + i|$ = 5$\sqrt{2}$
- D. $|z + i|$ = $\sqrt{41}$