Câu hỏi và bài tập trắc nghiệm toán 12 bài Ôn tập chương 4 - số phức

Câu 1: Phần thực và phần ảo của số phức $z = (1 + \sqrt{3}i)^{2}$ là

• A. 1 và 3   
• B. 1 và -3   

• C. -2 và 2$\sqrt{3}$ 

• D. 2 và -2$\sqrt{3}$ .

Câu 2: Phần ảo của số phức $z = (1 + \sqrt{3}i)^{3}$ là

• A. 3$\sqrt{3}$  
• B. -3$\sqrt{3}$ 
• C. – 8$i$   

• D. –8.

Câu 3: Thực hiện phép tính: T= $\frac{ 2+ 3i}{1+ i}+ \frac{3- 4i}{1- i}+ i(4+ 9i)$

Ta có: 

• A. T = $3 + 4i $  

• B. T = $-3 + 4i   $

• C. T = $3 – 4i   $
• D. T = $-3 – 4i$.

Câu 4: Phần thực và phần ảo của số phức $z$ thỏa mãn $(1 - i)z - 1 + 5i = 0$ là

• A. 3 và –2   

• B. 3 và 2   
• C. 3 và $– 2i  $ 
• D. 3 và $2i.$

Câu 5: Môđun của số phức z thỏa mãn điều kiện $(3z - \bar{z})(1 + i) - 5z = 8i - 1$ là

• A. 1   
• B. 5   

• C. $\sqrt{3}$     

• D. 13.

Câu 7: Tập hợp các điểm biểu diễn số phức $z$ thỏa mãn $|z - 2i|$ = 4 là

• A. Đường tròn tâm I(1; -2) bán kính R = 4
• B. Đường tròn tâm I(1; 2) bán kính R = 4

• C. Đường tròn tâm I(0; 2) bán kính R = 4

• D. Đường tròn tâm I(0; -2) bán kính R = 4

Câu 8: Tập hợp các điểm biểu diễn số phức $z$ thỏa mãn $|\bar{z}+ 3 - 2i|$ = 4 là

• A. Đường tròn tâm I(3; 2) bán kính R = 4
• B. Đường tròn tâm I(3; -2) bán kính R = 4
• C. Đường tròn tâm I(-3; 2) bán kính R = 4

• D. Đường tròn tâm I(-3; -2) bán kính R = 4

Câu 9: Gọi (H) là hình biểu diễn tập hợp các số phức $z$ trong mặt phẳng tọa độ $Oxy$ để $|2z- \bar{z}|$ số phức $z$ có phần thực không âm. Tính diện tích hình $(H)$.

• A. $3\pi$

• B. $\frac{3\pi}{2}$
• C. $\frac{3\pi}{4}$
• D. $6\pi$

Câu 10: Cho số phức z thỏa mãn $|z - 1 + 3i| + |z + 2 - i| = 8$. Tìm giá trị lớn nhất, giá trị nhỏ nhất của P = $|2z + 1 + 2i|$.

• A. max_P = 8; min_P = $\sqrt{39}$.   

• B. max_P = 10; min_P = $\sqrt{39}$.
• C. max_P = 8; min_P= 6.    
• D. max_P = 10; min_P = 6

Câu 11: Cho số phức z = a + bi, (a ≥ 0; b ≥ 0; a, b ∈ R). Đặt f(x) = ax2 + bx - 2.

Biết: $f(-1) \leq 0; f(\frac{1}{4}) \leq -\frac{5}{4}$

Tính giá trị lớn nhất của $|z|$ .

• A. max_$|z|$ = 2$\sqrt{5}$   

• B. max_$|z|$ = 3$\sqrt{2}$
• C. max_$|z|$ = 5    
• D. max_$|z|$ = 2$\sqrt{6}$

Câu 12: Cho số phức $z$ thỏa mãn $|z + 2 - i| + |z - 4 -7i| = 6\sqrt{2}$. Gọi $M, m$ lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức $P = |z - 1 + i|$. Giá trị của tổng $S = M + m$ là:

• A. $S= \frac{2\sqrt{29}+ 3\sqrt{2}}{2}$
• B. $\sqrt{13}+ \sqrt{73}$
• C. $5\sqrt{2}+ \sqrt{73}$

• D. $S= \frac{2\sqrt{73}+ 5\sqrt{2}}{2}$

Câu 13: Cho số phức $z$ thoả mãn $|z - 3 - 4i| = \sqrt{5}$. Gọi $M$ và $m$ là giá trị lớn nhất và giá trị nhỉ nhất của biểu thức $P = |z + 2|^{2} - |z - i|^{2}$. Tính module số phức $w = M + mi$

• A. $2\sqrt{314}$

• B. $\sqrt{1258}$

• C. $3\sqrt{137}$
• D. $2\sqrt{309}$

Câu 14: Cho hai số phức $z_{1}, z_{2}$ thỏa mãn $|3z- i|= |3+ iz|$. Biết rằng $|z_{1}- z_{2}|= \sqrt{3}$. Tính giá trị biểu thức $P= |z_{1}+ z_{2}|$

• A. $P= 2\sqrt{2}$
• B. $P= \frac{1}{2}$
• C. $P= \frac{3}{2}$

• D. $P= 1$

Câu 15: Cho số phức $z= x+ yi (x, y \in \mathbb{R})$ thỏa mãn: $z+ 1- 2i- |z|(1- i)= 0$. Trong mặt phẳng tọ độ $Oxy$, $M$ là điểm biểu diễn của số phức $z$. Khi đó $M$ thuộc đường thẳng nào sau đây? 

• A. $x- y+ 2= 0$

• B. $x+ y- 1= 0$

• C. $x+ y- 2= 0$
• D. $x+ y+ 1= 0$

Câu 16: Cho hai số phức $z. z'$ thỏa mãn $|z+ 5|= 5, |z'+ 1- 3i|= |z' - 3- 6i|$. Tìm giá trị nhỏ nhất của $|z- z|$

• A. $\frac{5}{2}$

• B. $\frac{5}{4}$
• C. $\sqrt{10}$
• D. $3\sqrt{10}$

Câu 17: Cho ba số phức $z_{1}, z_{2}, z_{3}$ không phải là số thực, thỏa mãn điều kiện $z_{1}+ z_{2}= 4$ và $|z_{1}- 2|= |z_{2}- 2|= |z_{3}- 2|$. 

Tính giá trị của biểu thức: $T= |z_{3}- z_{1}|^{2} + |z_{3}- z_{2}|^{2}$

• A. $T= 12$
• B. $T= 1$

• C. $T= 4$

• D. $T= 8$

Câu 18: Đường tròn ở hình dưới đây là tập hợp điểm biểu diễn cho số phức $z$ thỏa mãn đẳng thức nào sau đây?

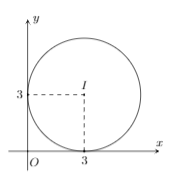
• A. $|z- 3|$= 3
• B. $|z|= 3$

• C. $|z- 3- 3i|$= 3

• D. $|z- 3i|$= 3

Câu 19: Gọi S là tập hợp tất cả các số phức thỏa mãn: $\left\{\begin{matrix}|\bar{z}- 2+ 5i|= 2&  & \\ |z- 5- i|= 3 &  & \end{matrix}\right.$

Hỏi tập S có bao nhiêu phần tử? 

• A. 0
• B. 2
• C. vô số

• D. 1

Câu 20: Cho số phức $z$. Gọi $A, B$ lần lượt là các điểm trong mặt phẳng $Oxy$ biểu diễn các số phức $z$ và $(1+ i)z$. Tính $|z|$ biết diện tích tam giác $OAB$ bằng 8.

• A. $|z|$= 4

• B. $|z|$= 2$\sqrt{2}$
• C. $|z|= 4\sqrt{2}$
• D. $|z|$= 2