Dạng 1: Xác định điểm cực đại, cực tiểu, giá trị cực đại, giá trị cực tiểu
Theo dõi 1.edu.vn trênPhần tham khảo mở rộng
Dạng 1: Xác định điểm cực đại ( $x_{CD}$), điểm cực tiểu ( $x_{CT}$), giá trị cực đại ($y_{CD}$), giá trị cực tiểu ($y_{CT}$) của hàm số.
Bài Làm:
I.Phương pháp giải:
Ta có thể dựa vào bảng biến thiên hoặc đồ thị hàm số để đi đến kết luận.
Chú ý không nhầm lẫn giữa các khái niệm:
- Điểm cực đại của hàm số, giá trị cực đại (cực đại) của hàm số, điểm cực đại của đồ thị hàm số và giá trị lớn nhất của hàm số;
- Điểm cực tiểu của hàm số, giá trị cực tiểu ( cực tiểu) của hàm số, điểm cực tiểu của đồ thị hàm số và giá trị nhỏ nhất của hàm số.
II.Bài tập áp dụng
Bài tập 1: Cho hàm số y = $f(x)$ liên tục trên $R$ , có đạo hàm $f^{'}$ = $x(x - 1)^{2}(x + 1)^{3}$. Hàm số có bao nhiêu điểm cực trị?
Bài giải:
Ta có bảng biến thiên:
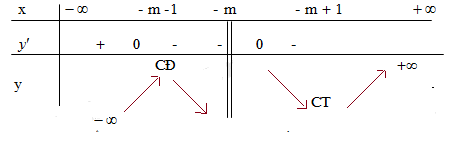
Nhìn vào bảng biến thiên ta thấy hàm số có hai điểm cực trị là x = -1 và x = 0.
Bài tập 2: Giá trị cực đại của hàm số y = $x^{3}$ - 3x + 1.
Bài giải:
Tập xác định : $D = R$.
Ta có: $y^{'}$ = $3x^{2} - 3$.
$y^{'}$ = 0 $\Leftrightarrow $ $3x^{2} - 3$ = 0 $\Leftrightarrow $ x = 1 hoặc x =-1.
x = 1 $\Rightarrow $ y = -1.
x = -1 $\Rightarrow $ y = 3.
Ta có các giới hạn : $\lim_{x \to-\infty }= -\infty $; $\lim_{x \to+\infty }= +\infty $.
Bảng biến thiên:
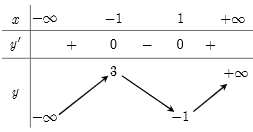
Từ bảng biến thiên ta thấy giá trị cực đại của hàm số là $y_{CD}$ = 3.