Dạng 2: Chứng minh các hệ thức vectơ
Theo dõi 1.edu.vn trênDạng 2: Chứng minh các hệ thức vectơ
Bài Làm:
I.Phương pháp giải
Sử dụng quy tắc ba điểm đối với phép cộng, phép trừ và các tính chất của các phép toán về vectơ để biến đổi các hệ thức vectơ.
II.Bài tập vận dụng
Bài tập 1: Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD, I là trung điểm của EF.
Bài giải:
a) Chứng minh rằng:
$\vec{IA}+\vec{IB}+\vec{IC}+\vec{ID}=0$.
b) Với điểm M bất kì trong không gian, hãy chứng minh rằng:
$4\vec{MI}=\vec{MA}+\vec{MB}+\vec{MC}+\vec{MD}$.
Bài giải:
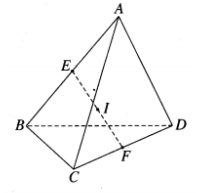
a) Ta có:
$\vec{IA}+\vec{IB}=2\vec{IE}$
$\vec{IC}+\vec{ID}=2\vec{IF}$
$\Rightarrow \vec{IA}+\vec{IB}+\vec{IC}+\vec{ID}=2(\vec{IE}+\vec{IF})$
Vì I là trung điểm của EF nên $\vec{IE}+\vec{IF}=0\Rightarrow \vec{IA}+\vec{IB}+\vec{IC}+\vec{ID}=0$. (đpcm)
b) Ta có:
$\vec{MI}=\vec{MA}+\vec{AI}$
$\vec{MI}=\vec{MB}+\vec{BI}$
$\vec{MI}=\vec{MC}+\vec{CI}$
$\vec{MI}=\vec{MD}+\vec{DI}$
$\Rightarrow 4\vec{MI}=\vec{MA}+\vec{MB}+\vec{MC}+\vec{MD}+\vec{AI}+\vec{BI}+\vec{CI}+\vec{DI}$
Mà theo câu a) ta có $\vec{IA}+\vec{IB}+\vec{IC}+\vec{ID}=0 \Rightarrow 4\vec{MI}=\vec{MA}+\vec{MB}+\vec{MC}+\vec{MD}$.
Bài tập 2: Cho tứ diện ABCD. Chứng minh rằng +
=
+
.
Bài giải:
Ta có:
$\vec{AC}=\vec{AD}+\vec{DC}$
$\vec{BD}=\vec{BC}+\vec{CD}$
$\Rightarrow \vec{AC}+\vec{BD}=\vec{AD}+\vec{DC}+\vec{BC}+\vec{CD}$
Mà $\vec{DC}+\vec{CD}=0$ nên $\vec{AC}+\vec{BD}=\vec{AD}+\vec{BC}$