Giá trị lớn nhất, giá trị nhỏ nhất của số phức
Theo dõi 1.edu.vn trênPhần tham khảo mở rộng
Dạng 1: Giá trị lớn nhất, giá trị nhỏ nhất của số phức
Bài Làm:
I. Phương pháp giải:
Chú ý công thức ||z₁| – |z₂|| ≤ |z₁ + z₂| ≤ |z₁ – z₂|.
II. Bài tập áp dụng
Bài tập 1: Cho số phức $z$ thoả mãn $|z-3-4i|=\sqrt{5}.$ Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=|z+2|^2-|z-i|^2.$ Tìm môđun của số phức $w= M+mi$.
Bài giải:
Ta có $|z-3-4i|=\sqrt{5} \Leftrightarrow (x-3)^2+(y-4)^2=5 ; (C)$
Tính toán ta được $P=|z+2|^2-|z-i|^2= 4x+2y+3.$ Xét đường thẳng $d: 4x+2y+3-P=0.$
Đường thẳng d và đường tròn (C) có điểm chung khi và chỉ khi
$d(I; d)\leq R \Leftrightarrow |23-P|\leq 10 \Leftrightarrow 13\leq P\leq 33.$
Vậy $M=33$; $m=13.$ Khi đó $w=33+13i$ nên $|w|=\sqrt{1248}.$
Bài tập 2: Cho số phức $z$ thoả mãn $|z^2-2z+5|=|(z-1+2i)(z+3i-1)|$. Tính $\min |w|$ với số phức $w=z-2+2i.$
Bài giải:
Ta có $z^2-2z+5=(z-1)^2+4=(z-1)^2-(2i)^2 =(z-1+2i)(z-1-2i).$
Khi đó, giả thiết $ \Leftrightarrow |(z-1+2i)(z-1-2i)|=|(z-1+2i)(z+3i-1)|$
$\Leftrightarrow \left[\begin{array}{l}z=1-2i \\|z-1-2i|=|z+3i-1|\end{array}\right.$
TH1: Với z=1-2i, ta có w=z-2+2i=-1. Vậy $|w|=1$.
TH2: Với $|z-1-2i|=|z+3i-1|$ (*), đặt z=x+yi, ta có
$(*)\Leftrightarrow |x-1+(y-2)i|=|x-1+(y+3)i|$
$\Leftrightarrow (x-1)^2+(y-2)^2=(x-1)^2+(y+3)^2 \Leftrightarrow y=\frac{-1}{2}$
Do đó $w=z-2+2i=x-\frac{1}{2}i-2+2i=x-2+\frac{3}{2}i \Rightarrow |w|=\sqrt{(x+2)^2+\frac{9}{4}}\geq \frac{3}{2}.$
Vậy $\min |w|=\frac{3}{2}.$
Bài tập 3: Cho số phức $z$ thoả mãn $|z|=1.$ Tìm giá trị lớn nhất của biểu thức
$T=|z+1|+2|z-1|$.
Bài giải:
Gọi $z=x+yi \Rightarrow M(x; y).$
Và $A(-1; 0), B(1;0)$. Ta có $|z|=1 \Rightarrow |x+yi|=1 \Leftrightarrow x^2+y^2=1.$
$\Rightarrow M$ thuộc đường tròn đường kính AB.
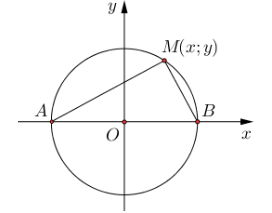
$\Rightarrow MA^2+MB^2=AB^2=4.$ Khi đó, theo Bunhiacopxki, ta có
$T=MA + 2MB \leq \sqrt{(1^2+2^2)(MA^2+MB^2)}=\sqrt{5.4}=2\sqrt{5}$.
Vậy $Max T= 2\sqrt{5}.$
Bài tập 4: Trong các số phức $z$ thoả mãn điều kiện $|z-2-4i|=\sqrt{5}.$ Tìm Max $|z|$; $\min |z|$.
Bài giải:
Vì $|z-2-4i|=\sqrt{5}$ nên tập hợp các điểm $M(z)$ là đường tròn $(C)$ có tâm $I(2;4)$ và bán kính $R=\sqrt{5}.$
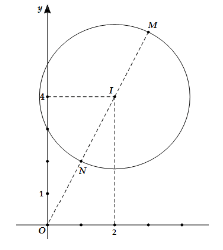
Vậy $Max |z|=OM=OI+R=\sqrt{2^2+4^2}+\sqrt{5}=3\sqrt{5}.$
$\min |z|=ON=OI-R=sqrt{2^2+4^2}-\sqrt{5}=\sqrt{5}.$
Bài tập 5: Trong các số phức $z$ thoả mãn điều kiện $|z-5i|\leq 3.$ Tìm số phức có môđun nhỏ nhất.
Bài giải:
Tập hợp các điểm $M(z)$ là hình tròn $(C)$ tâm $I(0;5)$ và bán kính R=3.
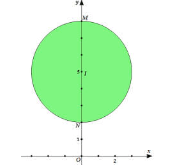
Vậy số phức z có môđun nhỏ nhất là $z=2i.$