Giải bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

A. Lí thuyết

1. Định nghĩa

Cho hàm số $y=f(x)$ xác định trên tập D.

• Số M được gọi là giá trị lớn nhất của hàm số $y=f(x)$ trên tập D nếu $f(x) \leq M$ với mọi x thuộc D và tồn tại $x_{0} \in D$ sao cho $f(x_{0}=M$. Kí hiệu $M=\max_{D} f(x)$.
• Số m được gọi là giá trị nhỏ nhất của hàm số $y=f(x)$ trên tập D nếu $f(x) \geq m$ với mọi x thuộc D và tồn tại $x_{0} \in D$ sao cho $f(x_{0}=m$. Kí hiệu $m=\min_{D} f(x)$.

2. Cách tính GTLN và GTNN của hàm số trên một đoạn

Định lí: Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.

Quy tắc tìm GTLN và GTNN của hàm số liên tục trên một đoạn

1. Tìm các điểm $x_{1}, x_{2},...,x_{n}$ trên khoảng (a,b) tại đó $f'(x)=0$ hoặc $f'(x)$ không xác định.
2. Tính $f(a), f(x_{1}), f(x_{2}),..., f(x_{n}),f(b)$.
3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có $M=\max_{[a,b]}f(x), m=\min_{[a,b]}f(x)$.

Tổng quát: Muốn tìm GTLN và GTNN của một hàm số trên TXĐ.

• Bước 1: Tìm TXĐ
• Bước 2: Giải phương trình $f'(x)=0$
• Bước 3: Lập bảng biến thiên
• Bước 4: Dựa vào bảng biến thiên đưa ra kết luận.

Ví dụ: Tìm GTLN và GTNN của hàm số $$y=x-5+\frac{1}{x}$$ trên khoảng $(0,+\infty)$.

Giải: TXĐ $D=(0,+\infty)$.

Ta có $y'=1-\frac{1}{x^{2}}=\frac{x^{2}-1}{x^{2}}=0\Leftrightarrow x=1$.

Bảng biến thiên

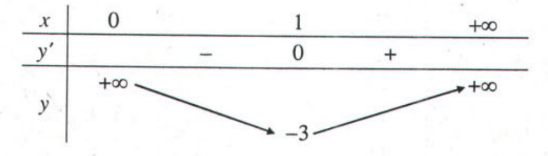
Từ bảng biến thiên ta thấy trên khoảng $(0,+\infty)$, hàm số đạt GTNN là -3 khi x=1 và không tồn tại giá trị lớn nhất của f(x) trên khoảng $(0,+\infty)$.