Giải bài: Ôn tập chương 4 - số phức
Theo dõi 1.edu.vn trênA. Tổng hợp kiến thức
Số phức
- Mỗi biểu thức dạng $a+bi$, ( $a,b \in R,i^{2}=-1$ ) là một số phức.
- $a$ gọi là phần thực của số phức $a+bi$.
- $b$ gọi là phần ảo của số phức $a+bi$.
- Ký hiệu tập số phức: $C$
-
$a+bi=c+di<=> a=c , b=d$
Các phép tính với số phức
- Phép cộng và phép trừ
| $(a+bi)+(c+di)=(a+c)+(b+d)i$ $(a+bi)-(c+di)=(a-c)+(b-d)i$ |
- Phép nhân
| $(a+bi)(c+di)=(ac-bd)+(ad+bc)i$ |
- Phép chia
| $z=\frac{c+di}{a+bi}$ |
- Tổng của một số phức với số phức liên hợp của nó bằng hai lần phần thực của số phức đó.
| $z+\overline{z}=(a+bi)+(a-bi)=2a$ |
- Tích của một số phức với số phức liên hợp của nó bằng bình phương môđun của số phức đó.
| $z.\overline{z}=(a+bi).(a-bi)=a^{2}-(bi)^{2}=a^{2}+b^{2}=\left | z \right |^{2}$ |
III. Phương trình bậc hai với hệ số thực
Cho phương trình bậc hai $ax^{2}+bx+c=0$, với $a,b,c \in R,a\neq 0$ .
Xét $\Delta =b^{2}-4ac$
- $\Delta =0$ => Phương trình có một nghiệm thực là: $x=-\frac{b}{2a}$.
- $\Delta >0$ => Phương trình có hai nghiệm thực là: $x_{1},_{2}=\frac{-b\pm \sqrt{\Delta }}{2a}$.
- $\Delta <0$ => Phương trình vô nghiệm.
B. Bài tập & Lời giải
Câu 2: Trang 143-sgk giải tích 12
Thế nào là phần thực phần ảo, mô đun của một số phức? Viết công thức tính mô đun của số phức theo phần thực phần ảo của nó?
Xem lời giải
Câu 3:Trang 143-sgk giải tích 12
Tìm mối liên hệ giữa khái niêm mô đun và khái niệm giá trị tuyệt đối của số thực.
Xem lời giải
Câu 4 :Trang 143-sgk giải tích 12
Nêu định nghĩa số phức liên hợp với số phức z. Số phức nào bằng số phức liên hợp của nó?
Xem lời giải
Câu 1:Trang 143-sgk giải tích 12
Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình a, b , c?
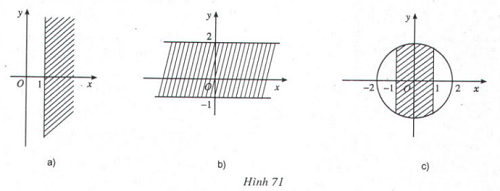
Xem lời giải
Câu 5:Trang 143-sgk giải tích 12
Trên mặt phẳng tọa độ, tìm tập hợp biểu diễn của các số phức z thỏa mãn điều kiện:
a) Phần thực của z bằng 1.
b) Phần ảo của z bằng -2.
c) Phần thực của z thuộc đoạn [-1; 2], phần ảo của z thuộc đoạn [0; 1].
d) $|z|\leq 2$
Xem lời giải
Câu 6:Trang 143-sgk giải tích 12
Tìm các số thực x, y sao cho:
a) $3x+yi=2y+1+(2-x)i$
b) $2x+y-1=(x+2y-5)i$
Xem lời giải
Câu 7:Trang 143-sgk giải tích 12
Chứng tỏ rằng với mọi số thực z, ta luôn có phần thực và phần ảo của nó không vượt quá mô đun của nó.
Xem lời giải
Câu 8 :Trang 143-sgk giải tích 12
Thực hiện các phép tính sau:
a) $(3 + 2i)[(2 – i) + (3 – 2i)]$
b) $(4-3i)+\frac{1+i}{2+i}$
c) $(1 + i)^{2}– (1 – i)^{2}$
d) $\frac{3+i}{2+i}-\frac{4-3i}{2-i}$
Xem lời giải
Câu 9:Trang 144-sgk giải tích 12
Giải tích phương trình sau trên tập số phức
a) $(3 + 4i)x + (1 – 3i) = 2 + 5i$
b) $(4 + 7i)x – (5 – 2i) = 6ix$
Xem lời giải
Câu 10:Trang 144-sgk giải tích 12
Giải các phương trình sau trên tập số phức
a) $3x^{2} + 7x + 8 = 0$
b) $x^{4} – 8 = 0$
c) $x^{4}– 1 = 0$
Xem lời giải
Câu 11:Trang 144-sgk giải tích 12
Tìm hai số phức, biết tổng của chúng bằng 3 và tích của chúng bằng 4.
Xem lời giải
Câu 12:Trang 144-sgk giải tích 12
Cho hai số phức $z_{1}, z_{2}$. Biết rằng $z_{1}+ z_{2}$ và $z_{1}.z_{2}$ là hai số thực.
Chứng minh rằng $z_{1}, z_{2}$ là hai nghiệm của một phương trình bậc hai với hệ số thực.