Giải bài: Ôn tập chương III - phương pháp tọa độ trong không gian
Theo dõi 1.edu.vn trênA. Tổng hợp kiến thức
I. Biểu thức tọa độ của các phép toán vectơ
- Trong không gian Oxyz cho hai vectơ $\overrightarrow{a}(a_{1};a_{2};a_{3})$ và $\overrightarrow{b}(b_{1};b_{2};b_{3})$. Ta có:
| $\overrightarrow{a}+\overrightarrow{b}=(a_{1}+b_{1};a_{2}+b_{2};a_{3}+b_{3})$ $\overrightarrow{a}-\overrightarrow{b}=(a_{1}-b_{1};a_{2}-b_{2};a_{3}-b_{3})$ $k\overrightarrow{a}=k(a_{1};a_{2};a_{3})$ với k là số thực |
==> Hệ quả:
| $\overrightarrow{a}=\overrightarrow{b}<=>a_{1}=b_{1};a_{2}=b_{2};a_{3}=b_{3}$ $\overrightarrow{0}=(0;0;0)$ $\overrightarrow{a},\overrightarrow{b}$ cùng phương <=> $a_{1}=kb_{1};a_{2}=kb_{2};a_{3}=kb_{3}$ $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=(x_{B}-x_{A};y_{B}-y_{A};z_{B}-z_{A})$ |
II. Tích vô hướng
Định lí
- Trong không gian Oxyz, tích vô hướng của hai vectơ $\overrightarrow{a}(a_{1};a_{2};a_{3})$ và $\overrightarrow{b}(b_{1};b_{2};b_{3})$ xác định bởi:
| $\overrightarrow{a}.\overrightarrow{b}=(a_{1}.b_{1}+a_{2}.b_{2}+a_{3}.b_{3})$ |
Ứng dụng
- Độ dài vectơ:
| $\overrightarrow{a}=\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}$ |
- Khoảng cách giữa hai điểm: Trong không gian Oxyz cho $A(x_{A},y_{A},z_{A})$ và $B(x_{B},y_{B},z_{B})$, ta có:
| $AB=\left | \overrightarrow{AB} \right |=\sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}+(z_{B}-z_{A})^{2}}$ |
- Góc giữa hai vectơ: Góc giữa $\overrightarrow{a}(a_{1};a_{2};a_{3})$ và $\overrightarrow{b}(b_{1};b_{2};b_{3})$ là $\varphi $
| $\cos\varphi =\cos (\overrightarrow{a},\overrightarrow{b})=\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}.\sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}$ |
- Đặc biệt:
| $\overrightarrow{a}\perp \overrightarrow{b}<=> a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}=0$ |
III. Phương trình mặt cầu
Định lí
- Trong không gian Oxyz, mặt cầu S có tâm I( a; b; c ) bán kính r có phương trình là:
| $(x-a)^{2}+(y-b)^{2}+(z-c)^{2}=r^{2}$ |
IV. Phương trình mặt phẳng
- Phương trình tổng quát của mặt phẳng:
| $Ax+By+Cz+D=0$ với $A,B,C\neq 0$. |
Điều kiện hai mặt phẳng song song, vuông góc
1. Điều kiện hai mặt phẳng song song
- $(\alpha _{1})//(\alpha _{2})<=>\left\{\begin{matrix}\overrightarrow{n_{1}}=k\overrightarrow{n_{2}} & \\ D_{1}\neq kD_{2} & \end{matrix}\right.<=> \left\{\begin{matrix}(A_{1};B_{1};C_{1})=k(A_{2};B_{2};C_{2}) & \\ D_{1}\neq kD_{2} & \end{matrix}\right.$
- $(\alpha _{1})\equiv (\alpha _{2})<=>\left\{\begin{matrix}\overrightarrow{n_{1}}=k\overrightarrow{n_{2}} & \\ D_{1}= kD_{2} & \end{matrix}\right.<=> \left\{\begin{matrix}(A_{1};B_{1};C_{1})=k(A_{2};B_{2};C_{2}) & \\ D_{1}= kD_{2} & \end{matrix}\right.$
- $(\alpha _{1})$ cắt $(\alpha _{2})$ <=> $\overrightarrow{n_{1}}\neq k\overrightarrow{n_{2}}<=>(A_{1};B_{1};C_{1})\neq k(A_{2};B_{2};C_{2}) $
2. Điều kiện hai mặt phẳng vuông góc
- $(\alpha _{1})\perp (\alpha _{2})<=>\overrightarrow{n_{1}}.\overrightarrow{n_{2}}=0<=>A_{1}.A_{2}+B_{1}.B_{2}+C_{1}.C_{2}=0$
Khoảng cách từ một điểm đến một mặt phẳng
Định lí
- Trong không gian Oxyz, cho mp($(\alpha )$ có phương trình $Ax+By+Cz+D=0$ và điểm $M_{0}(x_{0};y_{0};z_{0})$. Khoảng cách từ M đến mp($(\alpha )$ xác định bởi công thức:
| $d(M_{0},(\alpha ))=\frac{\left | Ax_{0}+By_{0}+Cz_{0}+D \right |}{\sqrt{A^{2}+B^{2}+C^{2}}}$ |
V. Phương trình tham số của đường thẳng
- Điều kiện cần và đủ để điểm $M(x;y;z)$ nằm trên $\Delta $ là có một số thực $t$ sao cho:
| $\left\{\begin{matrix}x=x_{0}+ta_{1} & & \\ y=y_{0}+ta_{2} & & \\ z=z_{0}+ta_{3} & & \end{matrix}\right.$ |
Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau
1. Hai đường thẳng song song
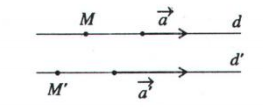
- d // d' <=> $d//d'<=>\left\{\begin{matrix}\overrightarrow{a}=k\overrightarrow{a'} & & \\ M \in d & & \\ M \notin d' & & \end{matrix}\right.$
- $d \equiv d'<=>\left\{\begin{matrix}\overrightarrow{a}=k\overrightarrow{a'} & & \\ M \in d & & \\ M \in d' & & \end{matrix}\right.$
2. Hai đường thẳng cắt nhau
Cho d: $\left\{\begin{matrix}x=x_{0}+ta_{1} & & \\ y=y_{0}+ta_{2} & & \\ z=z_{0}+ta_{3} & & \end{matrix}\right.$ và d': $\left\{\begin{matrix}x=x_{0}'+t'a_{1}' & & \\ y=y_{0}'+t'a_{2}' & & \\ z=z_{0}'+t'a_{3}' & & \end{matrix}\right.$
- $d$ và $d'$ cắt nhau <=> $\left\{\begin{matrix}x_{0}+ta_{1}=x_{0}'+t'a_{1}' & & \\ y_{0}+ta_{2}=y_{0}'+t'a_{2}' & & \\ z_{0}+ta_{3}=z_{0}'+t'a_{3}' & & \end{matrix}\right.$ có đúng một nghiệm.
3. Hai đường thẳng chéo nhau
- $d$ và $d'$ chéo nhau <=> $\left\{\begin{matrix}x_{0}+ta_{1}=x_{0}'+t'a_{1}' & & \\ y_{0}+ta_{2}=y_{0}'+t'a_{2}' & & \\ z_{0}+ta_{3}=z_{0}'+t'a_{3}' & & \end{matrix}\right.$ vô nghiệm.
B. Bài tập & Lời giải
Câu 1: Trang 91 - sgk hình học 12
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1)
a) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.
b) Tìm góc giữa hai đường thẳng AB và CD.
c) Tính độ dài đường cao của hình chóp A.BCD.
Xem lời giải
Câu 2: Trang 91, 92 - sgk hình học 12
Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7)
a) Tìm tọa độ tâm I và bán kính r của mặt cầu (S).
b) Lập phương trình của mặt cầu (S).
c) Lập phương trình của mặt phẳng ($\alpha$) tiếp xúc với mặt cầu (S) tại điểm A.
Xem lời giải
Câu 3: Trang 92 - sgk hình học 12
Cho bốn điểm A(-2; 6; 3), B(1; 0; 6), C(0; 2; -1), D(1; 4; 0)
a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.
b) Tính chiều cao AH của tứ diện ABCD.
c) Viết phương trình mặt phẳng ($\alpha$) chứa AB và song song với CD.
Xem lời giải
Câu 4: Trang 92 - sgk hình học 12
Lập phương trình tham số của đường thẳng:
a) Đi qua hai điểm A(1, 0 , -3) và B( 3, -1, 0).
b) Đi qua điểm M(2,3, -5) và // với đường thẳng $\Delta $ .
phương trình $\Delta $ : $\left\{\begin{matrix}x=-2+2t & & \\ y=3-4t& & \\ z=-5t& & \end{matrix}\right.$
Xem lời giải
Câu 5: Trang 92 - sgk hình học 12
Cho mặt cầu(S) có phương trình $(x-3)^{2}+(y+2)^{2}+(z-1)^{2}=100$ và mặt phẳng ($\alpha$) có phương trình $2x – 2y – z + 9 = 0$. Mp($\alpha$) cắt mặt cầu (S) theo một đường tròn (C). Hãy xác định tọa độ tâm và tính bán kính của đường tròn (C).
Xem lời giải
Câu 6: Trang 92 - sgk hình học 12
Cho mặt phẳng ($\alpha $) có phương trình: $3x + 5y -z - 2 =0$ và đường thẳng (d) có phương trình:
$\left\{\begin{matrix}x=12+4t & & \\ y=9+3t& & \\ z=1+t& & \end{matrix}\right.$
a. Tìm giao điểm M của (d) và mặt phẳng($\alpha $)
b. Viết phương trình mặt phẳng ($\beta $) chứa điểm M và vuông góc với (d).
Xem lời giải
Câu 7: Trang 92, 93 - sgk hình học 12
Cho đường thẳng (d) có phương trình : $\left\{\begin{matrix}x=1+3t & & \\ y=-1+2t& & \\ z=3-5t& & \end{matrix}\right.$
Cho điểm A(-1, 2, -3) và $\vec{a}=(6,-2,-3)$.
a. Viết phương trình mặt phẳng ($\alpha $) chứa điểm A và vuông góc với giá của $\vec{a}$.
b. Tìm giao điểm của (d) và ($\alpha $).
c. Viết phương trình đường thẳng $\Delta $ đi qua điểm A , vuông góc với $\vec{a}$ và cắt (d).
Xem lời giải
Câu 8: Trang 93 - sgk hình học 12
Viết phương trình mặt phẳng ($\alpha $) tiếp xúc với mặt cầu (S): $x^{2}+y^{2}+z^{2}-10x+2y+26z+170=0$ và // với hai đường thẳng:
(d) : $\left\{\begin{matrix}x=-5+2t & & \\ y=1-3t& & \\ z=-13+2t& & \end{matrix}\right.$
(d') : $\left\{\begin{matrix}x=-7+3t & & \\ y=-1-2t& & \\ z=8& & \end{matrix}\right.$
Xem lời giải
Câu 9: Trang 93 - sgk hình học 12
Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M(1; -1; 2) trên mặt phẳng ($\alpha$): $2x – y + 2z + 11 = 0$.
Xem lời giải
Câu 10: Trang 93 - sgk hình học 12
Cho điểm M(2; 1; 0) và mặt phẳng ($\alpha$): $x + 3y – z – 27 = 0$. Tìm tọa độ điểm M' đối xứng với M qua ($\alpha$).
Xem lời giải
Câu 11: Trang 93 - sgk hình học 12
Viết phương trình đường thẳng ∆ vuông góc với mặt phẳng tọa độ Oxz và cắt hai đường thẳng:
(d) : $\left\{\begin{matrix}x=t & & \\ y=-4+t& & \\ z=3-t& & \end{matrix}\right.$ và (d') : $\left\{\begin{matrix}x=1-2t' & & \\ y=-3+t'& & \\ z=4-5t'& & \end{matrix}\right.$
Xem lời giải
Câu 12: Trang 93 - sgk hình học 12
Tìm tọa độ điểm A' đối xứng với điểm A(1; -2; -5) qua đường thẳng có phương trình (d):
$\left\{\begin{matrix}x=1+2t & & \\ y=-1-t& & \\ z=2t& & \end{matrix}\right.$.