Giải câu 5 bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Theo dõi 1.edu.vn trênCâu 5: Trang 44 - sgk giải tích 12
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: $y = -x^{3} + 3x + 1$
b) Dựa vào đồ thị (C), biện luận về số nghiệm của phương trình sau theo tham số m: $x^{3} - 3x + m = 0$
Bài Làm:
a) Khảo sát hàm số $y = -x^{3} + 3x + 1$
- Tập xác định: D = R
- Sự biến thiên:
Ta có: $y' = -3x^{2} + 3 = -3(x^{2} - 1)$
=> $y' = 0 <=> -3(x^{2} - 1) = 0 <=> x = ±1$
- Giới hạn: $\lim_{x \to -\infty }y=+\infty $
$\lim_{x \to +\infty }y=-\infty $
- Bảng biến thiên:
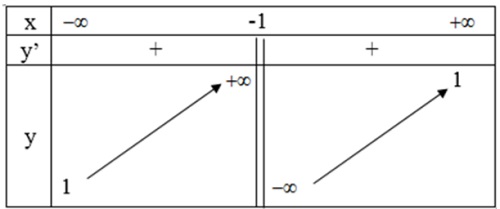
- Hàm số đồng biến trên khoảng (1; 1).
- Hàm số nghịch biến trên các khoảng (-∞; -1) và (1; +∞).
- Cực trị: Đồ thị hàm số có điểm cực tiểu là: (-1; -1).
Đồ thị hàm số có điểm cực đại là: (1; 3).
- Đồ thị:
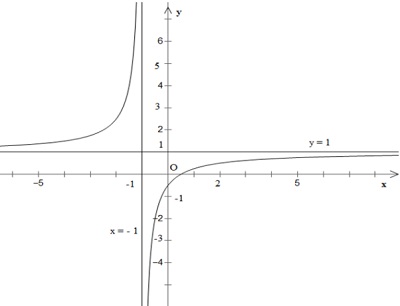
b) Ta có: $x^{3} - 3x + m = 0$ (*)
<=> $-x^{3} + 3x = m$
<=> $-x^{3} + 3x + 1 = m + 1$
Số nghiệm của phương trình (*) chính bằng số giao điểm của đồ thị hàm số (C) với đường thẳng (d): $y = m + 1$.
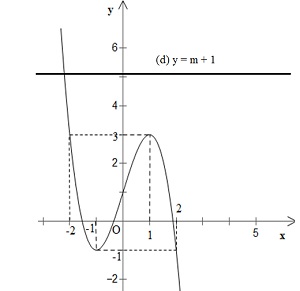
Biện luận:
- Nếu $m + 1 < –1 <=> m < –2$ thì (C ) cắt (d) tại 1 điểm.
- Nếu $m + 1 = –1 <=> m = –2$ thì (C ) cắt (d) tại 2 điểm.
- Nếu $–1 < m + 1 < 3 <=> –2 < m < 2$ thì (C ) cắt (d) tại 3 điểm.
- Nếu $m + 1 = 3 <=> m = 2$ thì (C ) cắt (d) tại 2 điểm.
- Nếu $m + 1 > 3 <=> m > 2$ thì (C ) cắt (d) tại 1 điểm.
=> Số nghiệm của phương trình $x^{3} - 3x + m = 0$ phụ thuộc tham số m.
- Phương trình có 1 nghiệm nếu $m < -2$ hoặc $m > 2$.
- Phương trình có 2 nghiệm nếu $m = -2$ hoặc $m = 2$.
- Phương trình có 3 nghiệm nếu $-2 < m < 2$.