Giải câu 9 bài: Ôn tập chương I

• TXĐ: D = R
• Sự biến thiên:

        Ta có:  $f'(x) = 2x^{3} - 6x = 2x(x^{2} - 3)$

         => $f'(x) = 0 <=> 2x(x^{2} - 3) = 0$

         <=> $x = 0; x=\pm \sqrt{3}$

• Giới hạn: $\lim_{x \to \pm \infty }f(x)=+\infty $
• Bảng biến thiên:

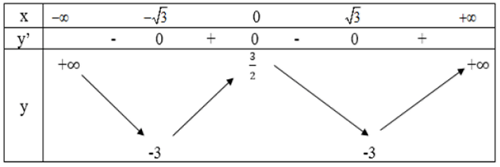
• Hàm số đồng biến trên $(-\sqrt{3}; 0)$ và $(\sqrt{3}3; +∞)$.
• Hàm số nghịch biến trên $(-∞; -\sqrt{3})$ và $(0; \sqrt{3})$.
• Cực trị: Đồ thị hàm số đạt cực đại tại (0; 3/2)

                         Đồ thị hàm số đạt cực tiểu tại (-√3; -3) và (√3; -3)

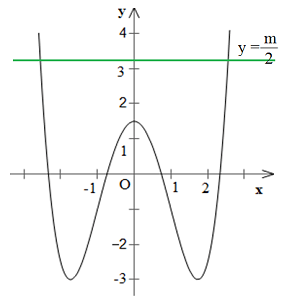
• Đồ thị:

b) Ta có: $f"(x) = 6x^{2} - 6 = 6(x^{2} - 1)$

=> #f"(x) = 0 <=> 6(x^{2} - 1)$

<=>  $x=\pm 1=> y=-1$

Phương trình tiếp tuyến của (C) tại $(-1; -1)$ là:  $y = f'(-1)(x + 1) - 1$

<=> $y = 4x + 3$

Phương trình tiếp tuyến của (C) tại $(1; -1)$ là: $y = f'(1)(x - 1) - 1$

<=> $y = -4x + 3$

c) Ta có: $x^{4} - 6x^{2} + 3 = m$

<=> $\frac{1}{2}x^{4}-3x^{2}+\frac{3}{2}=\frac{m}{2}$  (1)

=>Số nghiệm của phương trình (1) chính bằng số giao điểm của đồ thị (C) và đường thẳng $y =\frac{m}{2}$.

Biện luận: 

• $\frac{m}{2} < - 3 <=> m < -6$ => phương trình vô nghiệm.
• $\frac{m}{2} = -3 <=> m = -6$ => phương trình có 2 nghiệm.
• $\frac{m}{2}=\frac{3}{2} <=> m = 3$ => phương trình có 3 nghiệm.
• $\frac{m}{2}>\frac{3}{2} <=> m > 3$ => phương trình có 2 nghiệm.
• $-3 < \frac{m}{2} < \frac{3}{2} <=> -6 < m < 3$ => phương trình có 4 nghiệm.

==> Kết luận:

• $m < - 6$ thì phương trình vô nghiệm.
• $m = - 6$ hoặc $m > 3$ thì phương trình có 2 nghiệm.
• $m = 3$ thì phương trình có 3 nghiệm.
• $– 6 < m < 3$ thì phương trình có 4 nghiệm.