Lời giải bài số 39, 42, 48 Đề thi thử THPT quốc gia môn toán năm 2017- Đề tham khảo số 1
Theo dõi 1.edu.vn trênBài Làm:
HƯỚNG DẪN GIẢI
Câu 39: Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp. Nếu dung tích của cái hộp đó là $4800 cm^{3}$ thì cạnh của tấm bìa có độ dài là
| A. 42cm. | B. 36cm. | C. 44cm. | D. 38cm. |
Giải: Đáp án C
Đặt cạnh hình vuông là x, (x>24cm). Ta có
$4800=(x-24)^{2}.12 \Leftrightarrow x=44cm$.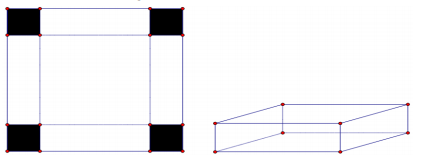
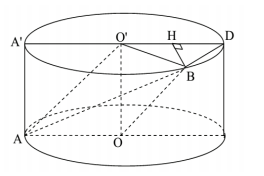
Câu 42: Cho hình trụ có các đáy là hai hình tròn có tâm O và O', bán kính đáy bằng chiều cao và bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tòn đáy tâm O' lấy điểm B sao cho AB=2a. Tính thể tích khối tứ diện OO'AB theo a.
| A. $V=\frac{\sqrt{3}a^{3}}{8}$. | B. $\frac{\sqrt{3}a^{3}}{6}$. | C. $\frac{\sqrt{3}a^{3}}{12}$. | D.$V=\frac{\sqrt{3}a^{3}}{4}$. |
Giải: Đáp án C
Kẻ đường sinh AA'. Gọi D là điểm đối xứng với $A'$ qua O' và H là hình chiếu của điểm B trên đường thẳng A'D.
Do $BH \perp A'D, BH \perp AA' \Rightarrow BH \perp (AOO'A')$
$A'B=\sqrt{AB^{2}-A'A^{2}}=a \sqrt{3} \Rightarrow BD= \sqrt{A'D^{2}-A'D^{2}}=a$.
$\bigtriangleup O'BD$ đều nên $BH=\frac{a\sqrt{3}}{2}$.
$S_{OO'A}=\frac{a^{2}}{2}$ suy ra $V_{OO'AB}=\frac{\sqrt{3}a^{3}}{12}.$
Câu 48: Gọi (S) là mặt cầu tâm $I(2,1,-1)$ và tiếp xúc với mặt phẳng $(\alpha): 2x-2y-z+3=0$. Bán kính của (S) bằng
| A. $\frac{4}{3}$. | B. $\frac{2}{9}$. | C. $\frac{2}{3}$. | D. $2$. |
Giải: Đáp án D
Bán kính R của mặt cầu (S) chính là khoảng cách từ tâm I của mặt cầu tới mặt phẳng $(\alpha)$:
$R=d(I,(\alpha ))=\frac{|2.2-2.1-(-1)+3}{\sqrt{2^{2}+(-2)^{2}+(-1)^{2}}}=2$.