Lời giải bài số 7, 9, 21 đề thi thử THPT Quốc gia môn toán năm 2017 của Sở Giáo dục và đào tạo tỉnh Hưng Yên
Theo dõi 1.edu.vn trênBài Làm:
Câu 7: Trong không gian với hệ trục tọa độ 0xyz, cho mặt phẳng (P): $2x-y-2z+1=0$ và ba điểm $A(1,-2,0), B(1,0,-1), C(0,0,-2)$. Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng (P) và tiếp xúc với ba đường thẳng AB, AC, BC?
A. 1 mặt cầu.
B. Vô số mặt cầu.
C. 4 mặt cầu.
D. 2 mặt cầu.
Giải: Đáp án C
Phương trình mặt phẳng (ABC): 2x-y-2z-4=0
Giả sử mặt cầu cần tìm có tâm I, bán kính R.
Gọi H, K, T, J lần lượt là hình chiếu của I lên AB, AC, BC, (ABC).
Theo tính chất tiếp xúc, ta có R=IH=IK=IT.
Suy ra 3 tam giác vuông $\Delta IJH=\Delta IJK=\Delta IJT (c-g-c)$ do đó JH=JK=JT suy ra J là tâm đường tròn nội tiếp hoặc bàng tiếp tam giác ABC. Vậy có 4 điểm J như vậy và ta sẽ có 4 điểm I tương ứng là hình chiếu của I lên (P). Tức là có 4 mặt cầu thỏa mãn.
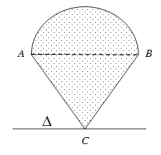
Câu 9: Cho hình phẳng (H) gồm nửa hình tròn đường kính AB và tam giác đều ABC như hình vẽ. Gọi $\Delta$ là đường thẳng qua C và song song với AB. Biết $AB=2 \sqrt{3} cm$. Tính thể tích khối tròn xoay tạo bởi hình (H) và trục $\Delta$.
A. $V=8 \sqrt{3}\pi +9 \pi^{2} cm^{3}$.
B. $V=8 \sqrt{3}\pi +\frac{9 \pi^{2}}{2} cm^{3}$.
C. $V=16 \sqrt{3}\pi +9 \pi^{2} cm^{3}$.
D. $V=16 \sqrt{3}\pi +\frac{27 \pi^{2}}{2} cm^{3}$.
Giải: Đáp án C
Chọn $C\equiv 0, \Delta \equiv 0x$, khi đó ta có tọa độ $A(-\sqrt{3},3), B(\sqrt{3},3)$ và phương trình đường tròn đường kính AB là $x^{2}+(y-3)^{2}=3$ và AC: $y=-\sqrt{3}x$, AB: $y=\sqrt{3}x$.
Phần phía trên của nửa đường tròn có phương trình $y=3+\sqrt{3-x^{2}}.$
Vì tính đối xứng của hình vẽ nên $V=2 \pi \int_{-\sqrt{3}}^{0} |(3+\sqrt{3-x^{2}})^{2}-(-\sqrt{3}x)^{2}|dx=16 \sqrt{3} \pi +9 \pi^{2}.
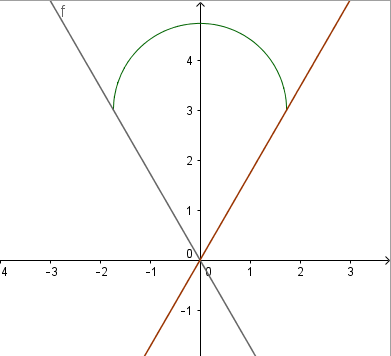
Câu 21: Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị của hàm số $y=f'(x)$ như hình vẽ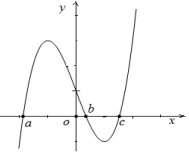
Chọn khẳng định đúng
A. $f(c)>f(b)>f(a)$.
B. $f(b)>f(c)>f(a)$.
C. $f(b)>f(a)>f(c)$.
D. $f(c)>f(a)>f(b)$.
Giải: Đáp án B
Chú ý theo định nghĩa tích phân và dựa vào đồ thị của hàm số, ta có diện tích của các hình phẳng:
$S_{1}=\int_{a}^{b}|f'(x)|dx=\int_{a}^{b}f'(x)dx=f(b)-f(a);$
$S_{2}=\int_{b}^{c}|f'(x)|dx=\int_{b}^{c}-f'(x)dx=f(b)-f(c);$
$S_{1}>S_{2}>0\Rightarrow f(b)>f(c)>f(a)$.