Lời giải câu 2, 3, 4 chuyên đề một số công thức tính nhanh bán kính mặt cầu ngoại tiếp hình chóp
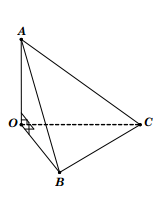
Theo dõi 1.edu.vn trênCâu 2: Cho tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc với nhau và OA=a, OB=2a, OC=2a. Tính bán kính mặt cầu ngoại tiếp tứ diện OABC.
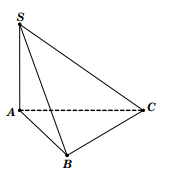
Câu 3: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, AB=a và $\widehat{BAC}=120^{0}$. Cạnh bên SA=2a và vuông góc với đáy (ABC). Tính bán kính mặt cầu ngoại tiếp hình chóp đã cho.
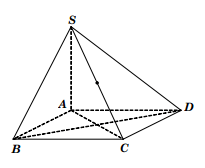
Câu 4: Cho hình chóp SABCD có đáy ABCD là hình vuông. SA vuông góc với mặt phẳng (ABCD) và SC=2a. Tính bán kính mặt cầu ngoại tiếp hình chóp trên.
Bài Làm:
Câu 3: Tam giác OBC vuông tại O nên $BC= \sqrt{OB^{2}+OC^{2}}= 2\sqrt{2} a \Rightarrow r= a \sqrt{2}$.
$h=OA=a$.
Áp dụng công thức ta có $R= \sqrt{(\frac{a}{2})^{2}+( a \sqrt{2})^{2}}= \frac{3a}{2}$.
Câu 4:Áp dụng Định lí cos ta có $BC=\sqrt{AB^{2}+AC^{2}-2.AB.AC.\cos \widehat{BAC}}=a \sqrt{3}$
Ta có $r=\frac{AB.AC.BC}{4.S_{ABC}}=\frac{AB.AC.BC}{2.AB.AC \sin \widehat{BAC}}=a$.
Áp dụng công thức ta có $R=\sqrt{(\frac{2a}{2})^{2}+a^{2}}=a\sqrt{2}.$
Câu 5: $r= \frac{AC}{2}$, $h=SA$
$R= \sqrt{(\frac{AC}{2})^{2}+(\frac{SA}{2})^{2}}=\frac{1}{2} SC=a.$