Một số bài tập liên quan đến hình vẽ đồ thị hàm số
Theo dõi 1.edu.vn trênA. Lí thuyết
I. Nhận dạng đồ thị
1. Phương pháp
- Thứ nhất: Đối với hàm bậc 3, trùng phương ta xem thử a> 0 hay a< 0, còn hàm bậc1/bậc 1 ta xem thử y’ >0 hay y’ <0 để có thể loại bớt những đáp án không phải.
- Thứ 2: Ta để ý đến tọa độ điểm thuộc đồ thị. (Khi nghi ngờ 1 hàm số nào ta phải điểm tra hết các điểm xem có thuộc vào hay không).
- Thứ 3: Đối với hàm phân thức ta nên để ý thêm các đường tiệm cận đứng và ngang của hàm số.
- Thứ 4: Một số dạng đồ thị ta phải kiểm tra thêm số điểm cực trị hoặc dựa vào BBT.
2. Một số hình dạng đồ thị đã học
a. Đồ thị hàm bậc ba
b. Đồ thị hàm bậc bốn trùng phương
c. Đồ thị hàm số $y=\frac{ax+b}{cx+d}$ $(c \neq 0, ad-bc \neq 0)$
ll. Dựa vào đồ thị hàm số tìm điểm cực trị, tính đơn điệu hàm số
Phương pháp: Quan sát hình vẽ nếu
- Đồ thị đi lên từ trái sang phải thì hàm số đồng biến.
- Đồ thị đi xuống từ trái sang phải thì hàm số nghịch biến.
- Tại điểm mà đồ thị chuyển từ đi lên sang đi xuống hoặc ngược lại.
B. Bài tập & Lời giải
 Câu 1: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Câu 1: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A. $y=x^{4}-2x^{2}-1$.
B. $y=x^{4}+2x^{2}+1$.
C. $y=x^{3}-3x^{2}-2$.
D. $y=-x^{3}+3x^{2}+2$.
Xem lời giải
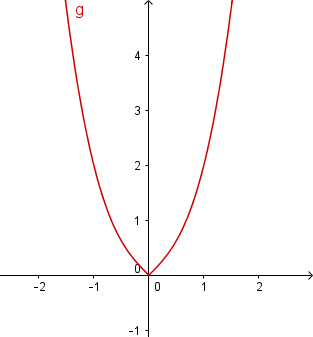
 Câu 2: Cho hàm số $y=ax^{3}+bx^{2}+cx+d$ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là đúng?
Câu 2: Cho hàm số $y=ax^{3}+bx^{2}+cx+d$ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là đúng?
A. $a<0, b>0, c>0, d<0$.
B. $a<0, b<0, c>0, d>0$.
C. $a>0, b<0, c<0, d>0$.
D. $a<0, b>0, c<0, d<0$.
Xem lời giải
 Câu 3: Cho hàm số $y=\frac{bx-c}{x-a} (a \neq 0, a, b, c \in \mathbb{R})$ có dạng như hình vẽ bên. Mệnh đề nào dưới đây là đúng?
Câu 3: Cho hàm số $y=\frac{bx-c}{x-a} (a \neq 0, a, b, c \in \mathbb{R})$ có dạng như hình vẽ bên. Mệnh đề nào dưới đây là đúng?
A. $a>0, b>0, c-ab<0$.
B. $a<0, b<0, c-ab>0$.
C. $a<0, b<0, c-ab<0$.
D. $a>0, b>0, c-ab>0$.
Xem lời giải
Câu 4: Trong các hàm số được cho bởi các đồ thị sau, hàm số nào đồng biến trên $\mathbb{R}$?
Xem lời giải
 Câu 5: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Câu 5: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A. $y=x^{3}-3x+1$.
B. $y=|x|(x^{2}+1)$.
C. $y=-x^{4}+2x$.
D. $y=\sqrt{x-1}$
Xem lời giải
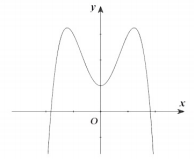 Câu 6: Cho hàm số $y=ax^{4}+bx^{2}+c (a \neq 0)$ có đồ thị như hình bên. Mệnh đề nào sau đây là đúng?
Câu 6: Cho hàm số $y=ax^{4}+bx^{2}+c (a \neq 0)$ có đồ thị như hình bên. Mệnh đề nào sau đây là đúng?
A. a<0, b<0, c<0.
B. a>0, b<0, c<0.
C. a>0, b<0, c>0.
D. a>0, b<0, c<0.
Xem lời giải
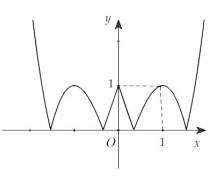 Câu 7: Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình bên. Số điểm cực trị của hàm số là
Câu 7: Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình bên. Số điểm cực trị của hàm số là
A. nhỏ hơn 5.
B. 6.
C. 7.
D. 8.
Xem lời giải
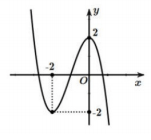 Câu 8: Hình bên là đồ thị của một hàm số trong bốn hàm số liệt kê dưới đây. Hàm số đó là hàm số nào?
Câu 8: Hình bên là đồ thị của một hàm số trong bốn hàm số liệt kê dưới đây. Hàm số đó là hàm số nào?
A. $y=x^{3}+3x^{2}-2$.
B. $y=x^{3}-3x^{2}-2$.
C. $y=-x^{3}-3x^{2}+2$.
D. $y=-x^{3}+3x^{2}+2$.
Xem lời giải
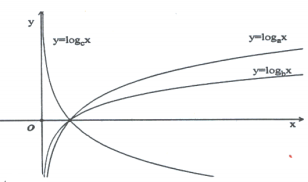 Câu 9: Cho ba số thực a, b, c khác 1. Đồ thị hàm số $y=\log_{a}x, y=\log_{b}x, y=\log_{c}x$ được cho trong hình vẽ bên.
Câu 9: Cho ba số thực a, b, c khác 1. Đồ thị hàm số $y=\log_{a}x, y=\log_{b}x, y=\log_{c}x$ được cho trong hình vẽ bên.
Mệnh đề nào sau đây là đúng?
A. b<c<a.
B. a<c<b.
C. c<a<b.
D. c<b<a.