Tìm điều kiện để hàm số đạt cực trị tại một giá trị
Theo dõi 1.edu.vn trênDạng 2: Cho hàm số $f_{m}(x)$ (m là tham số thực). Giả sử hàm số có đạo hàm tại $x_{0}$. Tìm tất cả những giá trị thực của m để hàm số đạt cực trị (cực tiểu, cực đại) tại x = $x_{0}$.
Bài Làm:
I.Phương pháp giải:
Sử dụng điều kiện cần: Nếu hàm số đạt cực trị tại x = $x_{0}$ thì $f_{m}^{'}(x_{0})$ = 0. Từ đây ta tìm được những giá trị thoả mãn điều kiện cần của m.
Ta thử lại mỗi giá trị của m vừa tìm được, kiểm tra hàm số có đạt cực trị tại x = $x_{0}$ hay không. Có hai cách:
Cách 1: sử dụng quy tắc 1 để khảo sát sự biến thiên của hàm số (sử dụng khi đạo hàm của hàm số dễ xét dấu);
Cách 2: sử dụng quy tắc 2, dựa vào đạo hàm cấp 2 ( sử dụng khi đạo hàm khó xét dấu).
II.Bài tập vận dụng
Bài tập 1: Tìm tất cả giá trị thực của m sao cho hàm số y = $\frac{x^{3}}{3} - \frac{1}{2}(m +2)x^{2}$ $+ (m^{2} - 5)x + 5.$ đạt cực trị tại x = -1.
Bài giải:
Ta có: $y^{'}$ = $x^{2} - (m +2)x + (m^{2} - 5).$
$\Rightarrow $ $y_{(-1)}^{'}$ = $m^{2} + m - 2$.
Điều kiện cần của m là: $y_{(-1)}^{'}$ = 0 $\Leftrightarrow $ m = 1 hoặc m = -2.
Thử lại:
m = 1: $y^{'} = x^{2} - 3x - 4.$. $y^{'}$ có hai nghiệm phân biệt là 4 và -1 (thoả mãn);
m = -2 : $y^{'} = x^{2} - 1.$. $y^{'}$ có hai nghiệm phân biệt là 1 và -1 (thoả mãn).
Vậy m = 1 hoặc m = -2.
Bài tập 2: Cho hàm số y = $\frac{x^{2} + mx + 1}{x + m}$. Tìm tất cả giá trị của m để hàm số:
a) đạt cực đại tại x = 2.
b) đạt cực tiểu và có $y_{CT}$ = 3.
Bài giải:
Tập xác định của hàm số: $D = R$ và $x \neq -m$ .
Ta có: $y^{'} = \frac{x^{2} + 2mx + m^{2} - 1}{(x + m)^{2}}$.
$y^{'}$ = 0 $\Leftrightarrow$ $x^{2} + 2mx + m^{2} - 1$ = 0 $\Leftrightarrow$ x = -m - 1 hoặc x = -m + 1
Ta có bảng biến thiên:
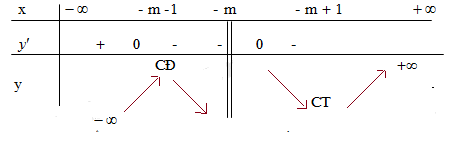
a) Theo bảng biến thiên ta thấy hàm số đạt cực đại tại x = -m - 1.
Hàm số đat cực đại tại x = 2 suy ra -m - 1 = 2 $\Leftrightarrow$ m = -3.
Vậy m = -3.
b) Hàm số đạt cực tiểu và có $y_{CT}$ = 3.
Nên $y_{CT}$ = -m + 1 = 3 $\Leftrightarrow$ m = -2.
Vậy m = -2.