Câu hỏi và bài tập trắc nghiệm toán 12 bài 3: Ứng dụng của tích phân trong hình học

Câu 1: Thể tích khối tròn xoay khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số $y = lnx, y = 0, x = 2 $ là:

• A. π(ln$^{2}$2 - 2ln2 + 1)    

• B. 2π(ln$^{2}$2 - 2ln2 + 1)

• C. 4π(ln$^{2}$2 - ln2 + 1)   
• D. 2π(ln$^{2}$2 - ln2 + 1)

Câu 2: Thể tích phần vật thể giới hạn bởi hai mặt phẳng $x = 0$ và $x = 3$ biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x(0 \leq x \leq 3)$ là một hình chữ nhật có hai kích thước là $x$ và 2$\sqrt{9-x^{2}}$

• A. $\frac{\sqrt{6}}{3}$

• B. 18

• C. $\frac{2\sqrt{3}}{3}$
• D. $\frac{3\sqrt{3}}{3}$

Câu 3: Vận tốc của một vật chuyển động là

                               v(t) = $\frac{1}{2\pi } + \frac{\sin (\pi t)}{\pi $  (m/s)

Quãng đường vật di chuyển trong khoảng thời gian 1,5 giây xấp xỉ bằng:

• A. 0,33m    

• B. 0,34m    

• C. 0,35m    
• D. 0,36m.

Câu 4: Diện tích hình phẳng được giới hạn bởi các đường y=lnx, trục hoành và hai đường thẳng x=$\frac{1}{e}$, x= $e$ là

• A. $e$+$\frac{1}{e}$ (dvdt)        
• B. 1-$\frac{1}{e}$ (dvdt)
• C. $e$  +$\frac{1}{e}$ (dvdt)        

• D. 2-$\frac{2}{e}$ (dvdt)

Câu 5: Cho hình phẳng (H) được giới hạn bởi đường cong (C):y=ex, trục Ox, trục Oy và đường thẳng x=2. Diện tích của hình phẳng (H) là

• A. e+4        
• B. $e^{2}$-e+2       
• C. $\frac{e^{2}}{2}$ + 3       

• D. $e^{2}$2-1

Câu 6: Diện tích hình phẳng giới hạn bởi các đường y=x$^{3}$, y=2-x$^{2}$, x=0 bằng:

• A. 17/12        
• B. -5/12        
• C.0        

• D. 12/17

Câu 7: Diện tích hình phẳng giới hạn bởi các đường (C): $ y= \frac{1}{4}x^{3} - x$ và tiếp tuyến của (C)tại điểm có hoành độ bằng-2, bằng:

• A. 27        

• B. 21        
• C. 11        
• D. 2

Câu 8: Diện tích hình phẳng giới hạn bởi các đường (C): $y= \frac{x^{2}-2x-15}{x-3}$ và hai trục toạ độ bằng:

• A. 12ln2 - $\frac{3}{2}$

• B. $\frac{256}{3}$
• C. 17 + 12ln3
• D. 16+ 12ln3

Câu 9: Diện tích hình phẳng giới hạn bởi các đường $y=\sin (2x), y=0, x=0, x= \pi $ bằng

• A. 2        

• B. 1        
• C. -1         
• D. -2

Câu 10: Diện tích hình phẳng giới hạn bởi các đường $y=-1, y=x^{4}-2x^{2}-1$ bằng

• A. $\frac{6\sqrt{2}}{5}$
• B. $\frac{28}{3}$

• C. $\frac{16\sqrt{2}}{15}$

• D. $\frac{27}{4}$

Câu 11: Cho đồ thị hàm số $y = f(x)$. Diện tích hình phẳng ( phần gạch sọc ) là:

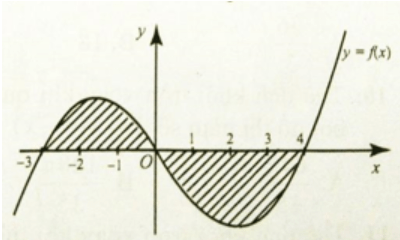
• A. $\int_{4}^{-3}f(x)dx$
• B. $\int_{1}^{-3}f(x)dx$ + $\int_{4}^{1}f(x)dx$

• C. $\int_{0}^{-3}f(x)dx$ + $\int_{4}^{0}[-f(x)dx]$

• D. $\int_{0}^{-3}f(x)dx$ + $\int_{4}^{0}f(x)dx$

Câu 12: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số$ y = \sqrt{x} - x$ và trục hoành.

• A. 1

• B. $\frac{1}{6}$

• C. $\frac{5}{6}$
• D. $\frac{1}{3}$

Câu 13: Gọi $h(t) (cm)$ là mức nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng

                               $h'(t) = \frac{1}{5} \sqrt[3]{t+ 8}$

và lúc đầu bồn không có nước. Mức nước ở bồn sau khi bơm nước được 6 giây xấp xỉ bằng:

• A. 2,66cm    

• B. 2,65cm

• C. 2,67cm    
• D. 2,68cm.

Câu 14: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số $y = f(x)$, trục Ox và hai đường thẳng $x = a, x = b (a < b)$ quanh trục $Ox$.

• A. $V= \pi \int_{b}^{a}f(x)dx$ 
• B. $v= \int_{b}^{a}f^{2}(x)dx$
• C. $V= \pi \int_{b}^{a}|f(x)|dx$

• D. $V= \pi \int_{b}^{a}f^{2}(x)dx$

Câu 15: Cho hàm số $y= f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ dưới đây: 

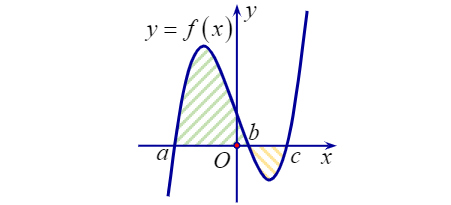
Hình phẳng được đánh dấu trong hình vẽ có diện tích là: 

• A. $\int_{b}^{a}f(x)dx - \int_{b}^{a}f(x)dx$

• B. $\int_{b}^{a}f(x)dx + \int_{c}^{b}f(x)dx$
• C. $-\int_{b}^{a}f(x)dx + \int_{c}^{b}f(x)dx$
• D. $\int_{b}^{a}f(x)dx - \int_{b}^{c}f(x)dx$

Câu 16: Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$, có đồ thị như hình vẽ. Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hàm số $f(x)$, trục hoành và trục tung. Khẳng định nào sau đây là đúng? 

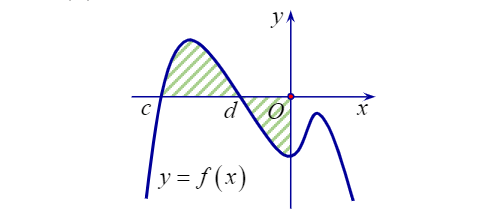
• A. $S= - \int_{d}^{c}f(x)dx+ \int_{0}^{d}f(x)dx$
• B. $S= -\int_{d}^{c}f(x)dx - \int_{0}^{d}f(x)dx$

• C. $S= \int_{d}^{c}f(x)dx- \int_{0}^{d}f(x)dx$$

• D. $S= \int_{d}^{c}f(x)dx + \int_{0}^{d}f(x)dx$

Câu 17: Diện tích của hình phẳng $H$ được giới hạn bởi đồ thị hàm số $y= f(x)$, trục hoành và hai đường thẳng $x=a, x=b (a<b)$ (phần tô đậm trong hình vẽ) tính theo công thức nào sau đây? 

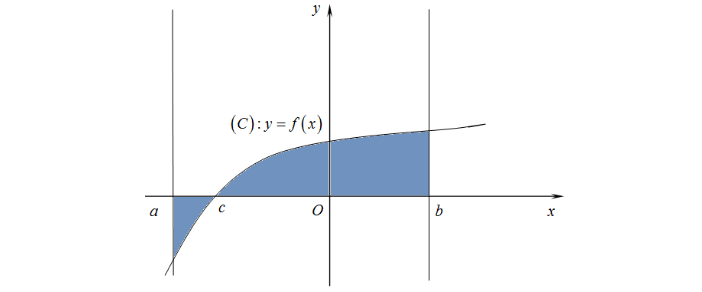
• A. $S= \int_{b}^{a}f(x)dx$

• B. $S= -\int_{c}^{a}f(x)dx + \int_{b}^{c}f(x)dx$

• C. $S= |\int_{b}^{a}f(x)dx|$
• D. $S= \int_{c}^{a}f(x)dx + \int_{b}^{c}f(x)dx$

Câu 18: Cho hàm số $y= f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị $(C)$ là đường cong như hình bên. Diện tích hình phẳng giới hạn bởi đồ thị $(C)$, trục hoành và hai đường thẳng $x= 0, x= 2$ (phần tô đen) là: 

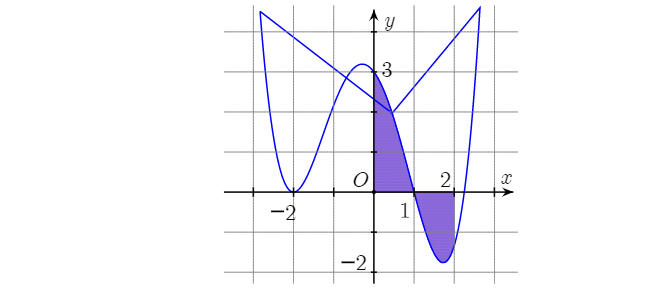
• A. $\int_{2}^{0}f(x)dx$
• B. $- \int_{1}^{0}f(x)dx + \int_{2}^{1}f(x)dx$

• C. $ \int_{1}^{0}f(x)dx- \int_{2}^{1}f(x)dx$

• D. $|\int_{2}^{0}f(x)dx|$

Câu 19: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số $y= e^{x} + e^{-x}$, trục hoành, trục tung và đường thẳng $x= -2$ là: 

• A. $S= \frac{e^{4}+ 1}{e^{2}}$ (đvdt)
• B. $S= \frac{e^{4}-1}{e}$ (đvdt)
• C. $S= \frac{e^{2}-1}{e}$ (đvdt)

• D. $S= \frac{e^{4}- 1}{e^{2}}$ (đvdt)

Câu 20: Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số $y= x^{3}$, trục hoành và hai đường thẳng $x= -1, x= 2$ biết rằng mỗi đơn vị dài trên các trục tọa độ bằng 2cm$

• A. 15 (cm$^{2}$)
• B. $\frac{15}{4}$ (cm$^{2}$)
• C. $\frac{17}{4}$ (cm$^{2}$)

• D. 17 (cm$^{2}$)