Câu hỏi và bài tập trắc nghiệm toán 12 bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số

NỘI DUNG TRẮC NGHIỆM

Câu 1: Đồ thị hàm số $y=a^{4}+bx^{2}+c$ ($a\neq 0$) có dạng sau:

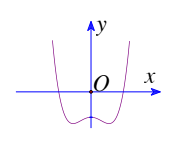
Xác định dấu của a, b, c

• A. a > 0; b < 0; c < 0. 

• B. a < 0; b < 0; c < 0.
• C. a > 0; b > 0; c < 0.
• D. a > 0; b < 0; c > 0.

Câu 2: Đồ thị hàm số $y=a^{4}+bx^{2}+c$ ($a\neq 0$) có dạng sau:

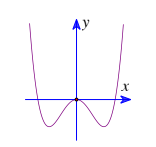
Xác định dấu của a, b, c.

• A. a > 0; b = 0; c = 0.
• B. a > 0; b > 0; c = 0.

• C. a > 0; b < 0; c = 0. 

• D. a < 0; b < 0; c = 0.

 Câu 3: Hàm số $y=ax^{3}+bx^{2}+cx+d$ có đồ thị như hình bên. Xác định dấu của a, b, c, d.

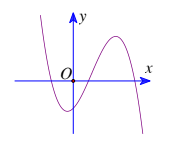
• A.  a< 0; b < 0; c > 0; d < 0.

• B.  a< 0; b > 0; c > 0; d < 0. 

• C.  a> 0; b > 0; c > 0; d < 0.
• D.  a< 0; b > 0; c > 0; d > 0.

Câu 4: Hàm số $y=ax^{3}+bx^{2}+cx+d$ có đồ thị như hình bên. Xác định dấu của a, b, c, d.

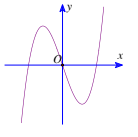
• A. a > 0; b = 0; c < 0; d = 0. 

• B. a < 0; b = 0; c < 0; d = 0.
• C. a > 0; b = 0; c > 0; d = 0.
• D. a > 0; b = 0; c < 0; d > 0.

Câu 5: Cho hàm số $y=-x^4+2x^2$ có đồ thị như hình vẽ. Tìm tất cả các giá trị thực của tham số $m$ để phương trình $-x^4+2 x^2=m$ có bốn nghiệm thực phân biệt.

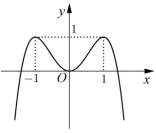
• A. $m>0.$
• B. $m<1.$

• C. $0<m<1.$ 

• D. $m<1.$

Câu 6: Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

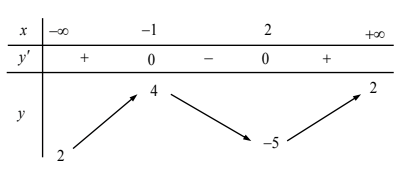
Mệnh đề nào dưới đây đúng?

• A. Hàm số có bốn điểm cực trị.

• B. Hàm số đạt cực tiểu tại $x=2$. 

• C. Hàm số không có cực đại.
• D. Hàm số đạt cực tiểu tại $x=-5$

Câu 7: Đường thẳng $y=3x+m$ là tiếp tuyến của đường cong $y=x^3+2$ khi m bằng

• A. 1 hoặc -1

• B. 4 hoặc 0 

• C. 3 hoặc -3
• D. 2 hoặc -2

Câu 8: CHo hàm số $y=f(x)$ có bảng xét dấu của đạo hàm như sau:

Mệnh đề nào dưới đây đúng?

• A. Hàm số đồng biến trên khoảng $(-2; 0)$.
• B. Hàm số đồng biến trên khoảng $(-\infty; 0)$.

• C. Hàm số nghịch biến trên khoảng $( 0; 2)$. 

• D. Hàm số nghịch biến trên khoảng $(-\infty; -2)$.

Câu 9: Đường cong dưới đây là đồ thị hàm số nào?

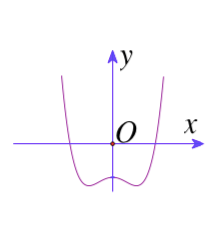
• A. $y=-x^3+x^2-1$.

• B. $y=x^4-x^2-1$. 

• C. $y=x^3-x^2-1$.
• D. $y=-x^4+x^2-1$.

Câu 10: Biết rằng đường thẳng $y=-2x+2$ cắt đồ thị hàm số $y= x^3+x+2$ tại một điểm duy nhất có toạ độ $(x_0; y_0)$. Tìm $y_0.$ 

• A. $y_0=4.$
• B. $y_0=0.$

• C. $y_0=2.$ 

• D. $y_0=-1.$

Câu 11: Phương trình đường thẳng đi qua các điểm cực trị của đồ thị hàm số $y=-x^3-3x^2+5x+1$ là:

• A. $y=\frac{-16x}{3}+\frac{34}{3}$.
• B. $y=\frac{-16x}{3}-\frac{34}{3}$.

• C. $y=\frac{16x}{3}-\frac{2}{3}$. 

• D. $y=\frac{16x}{3}+\frac{2}{3}$.

Câu 12: Với mọi $m \in (-1;1)$ phương trình $\sin^2 x +\cos x=m$ có mấy nghiệm trên đoạn $[0; \pi]$

• A. 0
• B. 1
• C. 2

• D. 3 

Câu 13: Với m>0 phương trình $|x|=\sqrt[3]{2x^2-|x|+m-1}$ có ít nhất mấy nghiệm

• A. 0 

• B. 1
• C. 2
• D. 3

Câu 14: Tìm m để phương trình $x^4-2x^2+3-m^2+2m=0$ có đúng 3 nghiệm phân biệt

• A. m=-1
• B. m=3
• C. m=2

• D. cả A và B