Dạng 3: Khối lăng trụ xiên

I.Phương pháp giải

Ta dựng đường cao từ một đỉnh, từ điều kiện đề bài ta tính đường cao và diện tích mặt đáy tương ứng để tính thể tích.

II.Bài tập vận dụng

Bài tập 1: Cho lăng trụ xiên tam giác $ABCA^{'}B^{'}C^{'}$ có đáy ABC là tam giác đều cạnh a, biết cạnh bên là $a\sqrt{3}$ và hợp với đáy một góc $60^{\circ}$. Tính thể tích lăng trụ.

Bài giải:

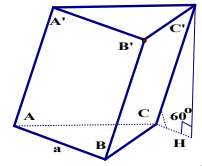
Ta dựng H là hình chiếu của $C^{'}$ trên (ABC) ta được CH là hình chiếu của $CC^{'}$ trên mặt phẳng (ABC).

Mà $CC^{'}$ tạo với (ABC) một góc $60^{\circ}$ nên $\widehat{C^{'}ÇH}=60^{\circ}$

Xét $\bigtriangleup C^{'}CH$ vuông tại H, có: $C^{'}H=CC^{'}.sin60^{\circ}=\frac{3a}{2}$.

$\bigtriangleup ABC$ đều nên ta có $S_{ABC}=\frac{a^{2}\sqrt{3}}{4}$.

Vậy $V= S_{ABC}. C^{'}H=\frac{3a}{2}.\frac{a^{2}\sqrt{3}}{4}=\frac{a^{3}3\sqrt{3}}{8}$.

Bài tập 2: Cho lăng trụ xiên tam giác $ABCA^{'}B^{'}C^{'}$ có đáy ABC là tam giác đều cạnh a. Hình chiếu của $A^{'}$ xuống (ABC) là tâm O đường tròn ngoại tiếp tam giác ABC, biết $AA^{'}$ hợp với đáy (ABC) một góc $60^{\circ}$. Tính thể tích lăng trụ.

Bài giải:

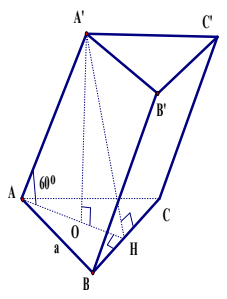
O là hình chiếu của $OA^{'}$ trên (ABC) nên OA là hình chiếu của $AA^{'}$ trên (ABC).

$\Rightarrow \widehat{(AA^{'},(ABC))}=\widehat{OAA^{'}}=60^{\circ}$.

Xét tam giác $AOA^{'}$ vuông tại O : $A^{'}O=AO.tan60^{\circ}=a$.

Tam giác ABC đều nên:

$S_{ABC}=\frac{a^{2}\sqrt{3}}{4}$

Vậy thế tích khối lăng trụ là:

$V=S_{ABC}.A^{'}O=a.\frac{a^{2}\sqrt{3}}{4}=\frac{a^{3}\sqrt{3}}{4}$.