Giải bài 6 vật lí 12: Thực hành khảo sát thực nghiệm các định luật của con lắc đơn
Theo dõi 1.edu.vn trênNội dung bài học gồm ba phần:
- Chuẩn bị thực hành và tiến hành thí nghiệm
- Viết báo cáo thực hành
- Trả lời câu hỏi và bài tập SGK trang 32
A. Chuẩn bị thực hành và tiến hành thí nghiệm
I. MỤC ĐÍCH
Khảo sát thực nghiệm để phát hiện ảnh hưởng của biên độ, khối lượng, chiều dài của con lắc đơn đối với chu kì dao động T, từ đó tìm ra công thức tính chu kì $T=2\pi \sqrt{\frac{l}{g}}$, và ứng dụng gia tốc trọng trường g tại nơi làm thí nghiệm.
II. DỤNG CỤ THÍ NGHIỆM
Chuẩn bị các dụng cụ gồm:
- Bộ ba quả nặng có móc treo loại 50g
- Một sợi dây mảnh không giãn dài khoảng 1m
- Một giá thí nghiệm dùng treo con lắc đơn có cơ cấu điều chỉnh chiều dài của con lắc đơn.
- Một đồng hồ bấm giây (sai số ± 0,2s) hoặc đồng hồ hiện số có cổng quang điện.
- Một thước đo chiều dài khoảng 500mm.
- Một tờ giấy kẻ ô milimet.
III. TIẾN HÀNH THÍ NGHIỆM
1. Chu kì dao động T của con lắc đơn phụ thuộc vào biên độ dao động như thế nào?
Tiến hành thí nghiệm:
- Mắc quả nặng m = 50g vào đầu tự do của sợi dây mảnh không dãn, điều chỉnh chiều dài con lắc đơn đúng bằng 50cm;
- Kéo con lắc lệch khỏi vị trí cân bằng biên độ A = 3cm, góc nghiêng $\alpha $;
- Đo thời gian con lắc thực hiện 10 dao động toàn phần (mỗi lần đo thời gian, ta đo lặp lại 5 lần, rồi lấy giá trung bình).
- Thực hiện phép đo trên với các giá trị khác nhau của biên độ A (A = 3, 6, 9, 18cm).
- Ghi kết quả vào bảng số liệu Bảng 6.1
Kết quả:
Bảng 6.1 m = 50g, l = 50,0cm
| A (cm) | $sin\alpha =\frac{A}{l}$ | Góc lệch $\alpha (^{0})$ | Thời gian 10 dao động t (s) | Chu kì T(s) |
| A1 =3,0 | 0,06 | 3,44 | t1 = 14,32 $\pm $ 0,32 | T1 = 1,432 $\pm $ 0,032 |
| A2 = 6,0 | 0,12 | 6,89 | t2 = 14,12 $\pm $ 0,2 | T2 = 1,412 $\pm $ 0,02 |
| A3 = 9,0 | 0,08 | 10,37 | t3 = 14,54 $\pm $ 0,24 | T3 = 1,454 $\pm $ 0,024 |
| A4 = 18 | 0,36 | 21.1 | t4 = 15,84 $\pm $ 0,31 | T4 = 1,584 $\pm $ 0,031 |
Rút ra định luật:
- Con lắc đơn dao động với biên độ nhỏ (α < 10$^{0}$) thì coi là dao động điều hòa, chu kỳ của con lắc khi đó không phụ thuộc vào biên độ dao động.
2. Chu kì dao động T của con lắc đơn phụ thuộc vào khối lượng m của con lắc như thế nào?
Tiến hành thí nghiệm:
- Chiều dài con lắc đơn cố định 50cm, thay đổi khối lượng của con lắc lần lượt là: 50; 100, 150g
- Đo thời gian 10 dao động toàn phần để xác định chu kì T
- Ghi kết quả vào bảng số liệu Bảng 6.2
Kết quả:
Bảng 6.2 l = 50,0cm; A = 3 cm
| m (g) | Thời gian 10 dao động t (s) | Chu kì T (s) |
| 50 | tA = 14,16 $\pm $ 0,26 | TA = 1,416 $\pm $ 0,026 |
| 100 | tB = 14,22 $\pm $ 0,2 | TB = 1,422 $\pm $ 0,02 |
| 150 | tC = 14,36 $\pm $ 0,28 | TC = 1,436 $\pm $ 0,028 |
Rút ra định luật:
- Chu kỳ của con lắc đơn dao động nhỏ (α < 10$^{0}$) không phụ thuộc vào khối lượng của con lắc.
3. Chu kì dao động T của con lắc đơn phụ thuộc vào chiều dài của con lắc như thế nào?
Tiến hành thí nghiệm:
- Dùng con lắc đơn có khối lượng là m = 50g, chiều dài là l = 50cm, Đo thời gian 10 dao động để xác định chu kì T1
- Thay đổi chiều dài con lắc đơn, giữ nguyên khối lượng, đo thời gian 10 dao động để tính chu kì T2 và T3
- Tính bình phương các chu kì $T_{1}^{2}, T_{2}^{2}, T_{3}^{2}$ và các tỉ số $\frac{T_{1}^{2}}{l_{1}}, \frac{T_{2}^{2}}{l_{2}}, \frac{T_{3}^{2}}{l_{3}}$.
- Ghi kết quả vào bảng số liệu Bảng 6.3
Kết quả:
Bảng 6.3
| Chiều dài l (cm) | Thời gian t = 10T (s) | Chu kì T(s) | $T^{2}(s^{2})$ | $\frac{T^{2}}{l}$ ($s^{2}$/cm) |
| l1 = 50,0 ± 0,1 | t1 = 14,29 ± 0,28 | T1 = 1,429 ± 0,028 | $T_{1}^{2}$ = 2,0420 ± 0,0800 | $\frac{T_{1}^{2}}{l_{1}}$ = 0,0408 ± 0,00168 |
| l2 = 45,0 ± 0,1 | t2 = 13,52 ± 0,24 | T2 = 1,352 ± 0,024 | $T_{2}^{2}$ = 1,8279 ± 0,0649 | $\frac{T_{2}^{2}}{l_{2}}$ = 0,0416 ± 0,00157 |
| l3 = 60,0 ± 0,1 | t3 = 15,78 ± 0,32 | T3 = 1,578 ± 0,032 | $T_{3}^{2}$ = 2,4900 ± 0,1010 | $\frac{T_{1}^{2}}{l_{3}}$ = 0,0415 ± 0,00175 |
- Vẽ đồ thị biểu diễn sự phụ thuộc của T vào l. Rút ra nhận xét
- Vẽ đồ thị biểu diễn sự phụ thuộc của $T^{2}$ vào l. Rút ra nhận xét
- Phát biểu định luật về chiều dài của con lắc đơn.
4. Kết luận
a) Từ các kết quả nhận được ở trên suy ra: Chu kỳ dao động của con lắc đơn với biên độ nhỏ, tại cùng một nơi, không phụ thuộc vào khối lượng và biên độ dao động của con lắc mà tỉ lệ với căn bậc hai chiều dài của con lắc theo công thức: $T=a\sqrt{l}$
Trong đó kết quả thí nghiệm cho ta giá trị a = 2,032
Theo công thức lí thuyết về chu kỳ dao động của con lắc đơn dao động với biên độ nhỏ:
$T=2\pi \sqrt{\frac{l}{g}}$ (*)
Trong đó $\frac{2\pi }{\sqrt{g}}\approx 2$ (với g lấy bằng 9,8m/$s^{2}$)
So sánh kết quả đo a cho thấy công thức (*) đã được nghiệm đúng.
c) Tính gia tốc trọng trường g tại nơi làm thí nghiệm theo giá trị a thu được từ thực nghiệm.
$g\frac{4\pi ^{2}}{a^{2}}=\frac{4\pi ^{2}}{2.0,032^{2}}=9,561$ (m/$s^{2}$)
B. Viết báo cáo thực hành
I. MỤC ĐÍCH THỰC HÀNH
- Phát hiện ảnh hưởng của biên độ, khối lượng, chiều dài con lắc đơn đối với chu kỳ dao động T.
- Từ đó tìm ra công thức $T=2\pi \sqrt{\frac{l}{g}}$ và ứng dụng tính gia tốc trọng trường g tại nơi làm thí nghiệm.
II. CƠ SỞ LÝ THUYẾT
1. Con lắc đơn có cấu tạo như thế nào? Chiều dài l của con lắc đơn được đo như thế nào?
Hướng dẫn:
- Con lắc đơn có cấu tạo gồm 1 vật nhỏ có khối lượng m được treo ở đầu của một sợi dây không dãn, khối lượng không đáng kể, dài l. Chiều dài 1 rất lớn so với kích thước quả cầu. Chiều dài của con lắc được xác định bằng cách đo khoảng cách từ điểm treo cố định đến trọng tâm của quả nặng.
- Chiều dài l của con lắc đơn được đo bằng thước đo của giá thí nghiệm dùng treo con lắc đơn có cơ cấu điều chỉnh chiều dài con lắc đơn.
2. Cần làm như thế nào để phát hiện ra sự phụ thuộc của chu kì dao động T của con lắc đơn dao động với biên độ nhỏ và biên độ dao động?
Hướng dẫn:
- Để phát hiện sự phụ thuộc của chu kì dao động T của con lắc đơn dao động với biên độ nhỏ vào biên độ dao động, ta xác định các chu kì dao động của cùng một con lắc với chiều dài 1 không đổi, nhưng có biên độ A thay đổi. Đo thời gian dao động có biên độ A khác nhau.
3. Cần làm như thế nào để phát hiện ra sự phụ thuộc của chu kì dao động T của con lắc đơn dao động với biên độ nhỏ và chiều dài l của con lắc đơn?
Hướng dẫn:
-
Để phát hiện sự phụ thuộc chu kỳ dao động T của con lắc đơn dao động với biên độ nhỏ vào chiều dài con lắc đơn ta khảo sát chu kỳ dao động T của con lắc đơn với chiều dài tăng dần, có 3 trường hợp có thể xảy ra:
+ l tăng thì T giảm
+ l tăng thì T không đổi hay l không phụ thuộcT
+ l tăng thì T tăng
4. Làm cách nào để xác định chu kì T với sai số ΔT = 0,02s khi dùng đồng hồ có kim giây? Cho biết sai số khi dùng đồng hồ này là $\pm $0,2s (gồm sai số chủ quan khi bấm và sai số dụng cụ).
Hướng dẫn:
- Để xác định chu kì T với sai số ΔT = 0,02s khi dùng đồng hồ có kim giây. Ta cần đo thời gian t của N dao động toàn phần.
- Trong quá trình đo t của đồng hồ kim giây có sai số là 0,2s bao gồm sai số chủ quan khi bấm và sai số dụng cụ nên Δt = n.ΔT = 0,2 + 0,02 = 0,22s, do đó cần đo số dao động toàn phần N > 11 dao động.
III. KẾT QUẢ
1. Khảo sát ảnh hưởng của biên độ dao động đối với chu kỳ T của con lắc đơn.
Hướng dẫn:
- Chu kỳ T1 = $\frac{t_{1}}{10}$ = 1,432s; T2 = $\frac{t_{2}}{10}$ = 1,412s; T3 = $\frac{t_{3}}{10}$ = 1,454s.
- Phát biểu định luật về chu kỳ của con lắc đơn dao động với biên độ nhỏ:
Con lắc đơn dao động với biên độ nhỏ (α < 10$^{0}$) thì coi là dao động điều hòa, chu kỳ của con lắc khi đó không phụ thuộc vào biên độ dao động.
2. Khảo sát ảnh hưởng của khối lượng của con lắc m đối với chu kỳ dao động T.
Hướng dẫn:
- Con lắc khối lượng mA có chu kỳ TA = 1,416 ± 0,026
- Con lắc khối lượng mB có chu kỳ TB = 1,422 ± 0,020
- Con lắc khối lượng mC có chu kỳ TC = 1,436 ± 0,028
- Phát biểu định luật về khối lượng của con lắc đơn:
Chu kỳ của con lắc đơn dao động nhỏ (α < 10$^{0}$) không phụ thuộc vào khối lượng của con lắc.
3. Khảo sát ảnh hưởng của chiều dài con lắc đơn l đối với chu kỳ dao động T
Hướng dẫn:
- Căn cứ các kết quả đo và tính được theo bảng 6.3, vẽ đồ thị biểu diễn sự phụ thuộc của T vào l và đồ thị của T2 vào l:
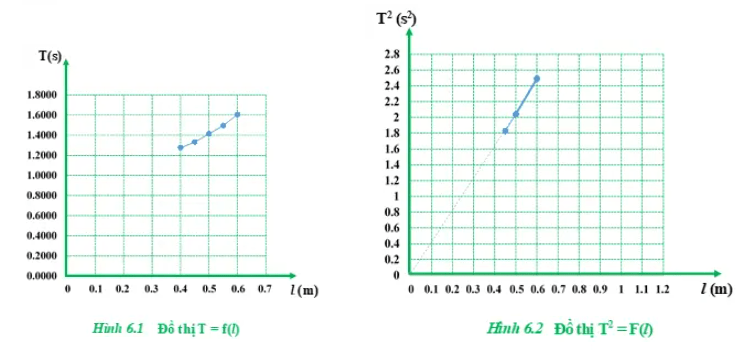
- Nhận xét:
a) Đường biểu diễn T = f(l) có dạng cong lên cho thấy rằng: Chu kỳ dao động T phụ thuộc đồng biến với độ dài con lắc đơn.
Đường biểu diễn T2 = F(l) có dạng đường thẳng qua gốc tọa độ cho thấy rằng: Bình phương chu kỳ dao động T$^{2}$ tỷ lệ với độ dài con lắc đơn. T$^{2}$ = k.l, suy ra $T=a\sqrt{l}$.
“Chu kỳ dao động của con lắc đơn với biên độ nhỏ, tại cùng một nơi, không phụ thuộc vào khối lượng và biên độ dao động của con lắc mà tỉ lệ với căn bậc hai chiều dài của con lắc theo công thức: $T=a\sqrt{l}$ với $a=\sqrt{k}$ trong đó a là hệ số góc của đường biểu diễn T$^{2}$ = F(l).
b) Công thức lí thuyết về chu kỳ dao động của con lắc đơn dao động với biên độ nhỏ: $T=2\pi \sqrt{\frac{l}{g}}$
Đã được nghiệm đúng, với tỉ số: $\frac{2\pi }{\sqrt{g}}=a=2,032$
Từ đó tính được gia tốc trọng trường g tại nơi làm thí nghiệm:
$g\frac{4\pi ^{2}}{a^{2}}=\frac{4\pi ^{2}}{2.0,032^{2}}=9,561$ (m/$s^{2}$)
4. Xác định công thức về chu kỳ dao động của con lắc đơn
Hướng dẫn:
Từ các kết quả thực nghiệm suy ra: Chu kỳ dao động của con lắc đơn dao động điều hòa với biên độ nhỏ không phụ thuộc vào khối lượng và biên độ dao động của con lắc mà tỉ lệ với căn bậc hai chiều dài l của con lắc đơn và tỉ lệ nghịch với căn bậc hai của gia tốc rơi tự do tại nơi làm thí nghiệm, hệ số tỉ lệ bằng $\frac{2\pi }{\sqrt{g}}$ $T=2\pi \sqrt{\frac{l}{g}}$.
C. Trả lời câu hỏi và bài tập SGK trang 32
1. Dự đoán xem chu kì dao động T của một con lắc đơn phụ thuộc vào những đại lượng đặc trưng l, m, α của nó như thế nào? Làm cách nào để kiểm tra từng dự đoán đó bằng thí nghiệm?
Hướng dẫn:
- Dự đoán chu kì T của con lắc đơn phụ thuộc vào những đại lượng đặc trưng chiều dài l, khối lượng vật nặng m, biên độ góc $\alpha _{0}$.
- Để kiểm tra từng dự đoán đó, ta cần tiến hành thí nghiệm thay đổi một đại lượng và giữ không đổi hai đại lượng còn lại.
2. Chu kì dao động của con lắc đơn có phụ thuộc vào nơi làm thí nghiệm hay không? Làm cách nào để phát hiện điều đó bằng thí nghiệm?
Hướng dẫn:
- Dự đoán chu kì dao động của con lắc đơn phụ thuộc vào nơi làm thí nghiệm.
- Để kiểm chứng dự đoán đó, ta cần tiến hành thí nghiệm với con lắc có chiều dài không đổi tại những nơi khác nhau.
3. Có thể đo chu kì con lắc đơn có chiều dài l < 10cm hay không? Vì sao?
Hướng dẫn:
- Không thể đo chu kì con lắc đơn có chiều dài nhỏ hơn 10cm
- Vì khi đó kích thước của quả nặng là đáng kể so với chiều dài dây, do đó khó tạo ra dao động với biên độ nhỏ dẫn đến khó đo chu kì T.
4. Dùng con lắc dài hay ngắn sẽ cho kết quả chính xác hơn khi xác định gia tốc rơi tự do g tại nơi làm thí nghiệm?
Hướng dẫn:
Dùng con lắc dài để xác định gia tốc trọng trường g cho kết quả chính xác hơn khi dùng con lắc ngắn vì sai số tỉ đối $\frac{\Delta g}{g}=\frac{2\Delta T}{T}+\frac{\Delta l}{l}$ có giá trị rất nhỏ.