Giải câu 37 bài: Ôn tập chương II
Theo dõi 1.edu.vn trênCâu 37: Trang 61, 62 - sgk hình học 12
a) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ:
$y = 0,5x + 2$ (1); $y = 5 – 2x$ (2)
b) Gọi giao điểm của các đường thẳng $y = 0,5x + 2$ và $y = 5 – 2x$ với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C.
Tìm tọa độ của các điểm A, B, C.
c) Tính độ dài các đoạn thẳng AB, AC và BC (đơn vị đo trên các trục tọa độ là xentimet) (làm tròn đến chữ số thập phân thứ hai).
d) Tính các góc tạo bởi các đường thẳng có phương trình (1) và (2) với trục Ox (làm tròn đến phút).
Bài Làm:
a) Vẽ đồ thị:
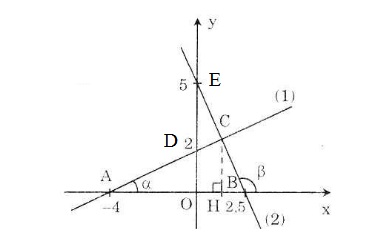
b) Ta có: A(-4; 0)
B(2,5; 0)
=> Hoành độ giao điểm C của hai đồ thị là nghiệm phương trình:
<=> $0,5x + 2 = 5 – 2x => x = 1,2$
=> $y = 0,5.1,2 + 2 = 2,6$
=> Tọa độ C(1,2 ; 2,6)
c) $AB = AO + OB = |-4| + |2,5| = 6,5 (cm)$
Gọi H là hình chiếu của C trên Ox
Ta có: $H( 1,2; 0)$
$AC=\sqrt{AH^{2}+CH^{2}}\approx 5,81$
$BC=\sqrt{BH^{2}+CH^{2}}\approx 2,91$
d) Gọi $\alpha$ là góc hợp bởi đường thẳng $y = 0,5x + 2$ với tia Ox.
Ta có: $ \tan \alpha = 0,5 => \alpha = 26^{\circ}34'$
Gọi $\beta$ là góc hợp bởi đường thẳng $y = 5 – 2x$ với tia Ox ($\beta$ là góc tù).
Gọi $\beta'$ là góc kề bù với $\beta$, ta có:
$\tan \beta' = -(-2) = 2 => \beta' =63^{\circ}26'$
=> $\beta = 180^{\circ}-63^{\circ}26'=116^{\circ}34'$