Trắc nghiệm hình học 12 bài 3: Khái niệm về thể tích của khối đa diện
Theo dõi 1.edu.vn trênCâu 1: Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a$\sqrt{2}$ . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k = V'/V?
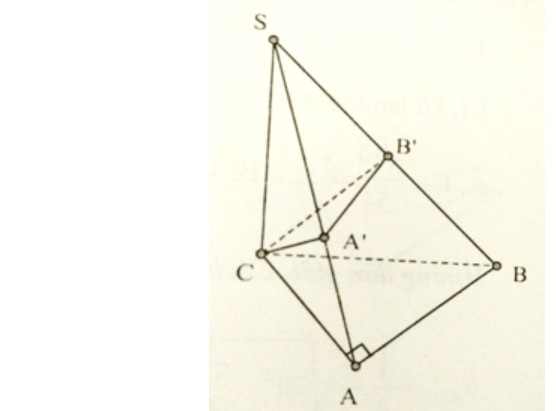
- A. $k= \frac{1}{3}$
- B. $k= \frac{\sqrt{2}}{4}$
-
C. $k= \frac{4}{9}$
- D. $k= \frac{2}{3}$
Câu 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a√2 , tam giác SAD cân tại S, mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích S.ABCD bằng 4a3/3. Tính khoảng cách h từ B đến mặt phẳng (SCD)
- A. $h= \frac{2}{3}$a
-
B. $h= \frac{4}{3}$a
- C. $h= \frac{8}{3}$a
- D. $h= \frac{3}{4}$a
Câu 3: Tính thể tích V của hình chóp tam giác đều S.ABC có cạnh đáy bằng a, mặt bên (SAB) tạo với đáy một góc bằng 60$^{o}$.
-
A. V= $\frac{\sqrt{3}}{24}$a$^{3}$
- B. V= $\frac{\sqrt{3}}{16}$a$^{3}$
- C. V= $\frac{\sqrt{3}}{12}$a$^{3}$
- D. V= $\frac{\sqrt{2}}{12}$a$^{3}$
Câu 4: Tính thể tích V của một tứ diện đều có cạnh bằng a.
-
A. V = $\frac{\sqrt{2}}{8}$a$^{3}$
-
B. V = $\frac{\sqrt{2}}{9}$a$^{3}$
-
C. V= $\frac{\sqrt{2}}{12}$a$^{3}$
-
D. V= $\frac{\sqrt{2}}{24}$a$^{3}$
Câu 5: Cho khối chóp S.ABC có đáy là tam giác đều cạnh a, hình chiếu của S lên mặt phẳng (ABC) trùng với trung điểm của cạnh AB, cạnh bên SC tạo với đáy một góc bằng 60o. Tính thể tích V của khối chóp đó.
-
A. V = $\frac{\sqrt{3}}{16}$a$^{3}$
-
B. V = $\frac{\sqrt{3}}{24}$a$^{3}$
-
C. V= $\frac{\sqrt{3}}{8}$a$^{3}$
-
D. V= $\frac{\sqrt{3}}{18}$a$^{3}$
Câu 6: Cho khối chóp S.ABC có đáy là tam giác đều cạnh a, hình chiếu của S lên mặt phẳng (ABC) trùng với trung điểm của cạnh AB, cạnh bên SC tạo với đáy một góc bằng 60$^{o}$. Tính thể tích V của khối chóp đó.
- A. V= $\frac{\sqrt{3}}{16}$a$^{3}$
- B. V= $\frac{\sqrt{3}}{24}$a$^{3}$
-
C. V= $\frac{\sqrt{3}}{8}$a$^{3}$
- D. V= $\frac{\sqrt{2}}{12}$a$^{3}$
Câu 7: Cho hình chóp S.ABC đáy là tam giác vuông tại A, SAB là tam giác đều cạnh a, hình chiếu của S lên mặt đáy trùng với trung điểm của AB, cạnh BC tạo với mặt bên (SAC) một góc 45$^{o}$ . Tính thể tích V của hình chóp đó.
- A. V= $\frac{\sqrt{2}}{8}$a$^{3}$
- B. V= $\frac{\sqrt{6}}{12}$a$^{3}$
-
C. V= $\frac{\sqrt{6}}{24}$a$^{3}$
- D. V= $\frac{\sqrt{3}}{24}$a$^{3}$
Câu 8: Cho hình chóp S.ABC có đáy làm tam giác vuông ở A, góc ACB = 30$^{o}$ . Hình chiếu của S lên đáy trùng với trọng tâm của tam giác ABC. SA tạo với dáy một góc bằng 60$^{o}$ và SA = 4. Tính thể tích V của hình chóp S.ABC
- A. V = 6
- B. V = 8
-
C. V = 9
- D. V = 12
Câu 9: Tính thể tích V của hình chóp tứ giác đều S.ABCD, diện tích mặt bên bằng $\frac{\sqrt{3}}{6}$a$^{2}$, góc giữa mặt bên và mặt đáy bằng 30$^{o}$
- A. V= $\frac{\sqrt{3}}{4}$a$^{3}$
- B. V= $\frac{\sqrt{3}}{6}$a$^{3}$
-
C. V= $\frac{\sqrt{3}}{18}$a$^{3}$
- D. V= $\frac{\sqrt{2}}{6}$a$^{3}$
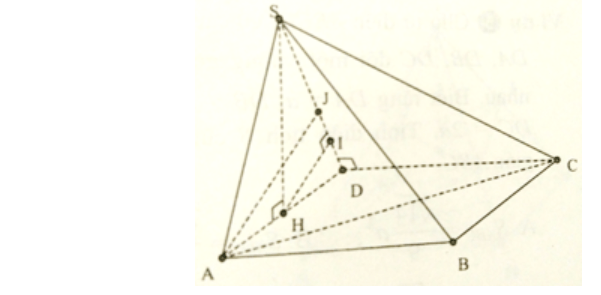
Câu 10: Cho hình chóp S.ABC có các cạnh bên đôi một vuông góc với nhau, SA= 6, SB = 4, SC = 5. Gọi M, P lần lượt là trung điểm của AB, CA. Tính thể tích của hình chóp S.MBCP
- A. V = 5
-
B. V = 15
- C. V = 30
- D. V = 45
Câu 11: Cho hình lăng trụ ABCD.A’B’C’D’có đáy ABCD là hình vuông cạnh bằng a. Hình chiếu vuông góc của điểm A’ trên mặt phẳng ABCD là trung điểm I của cạnh AB. Biết A’C tạo với mặt phẳng đáy một góc α với tanα=$\frac{2}{\sqrt{5}}$. Thể tích khối chóp A’.ICD là:
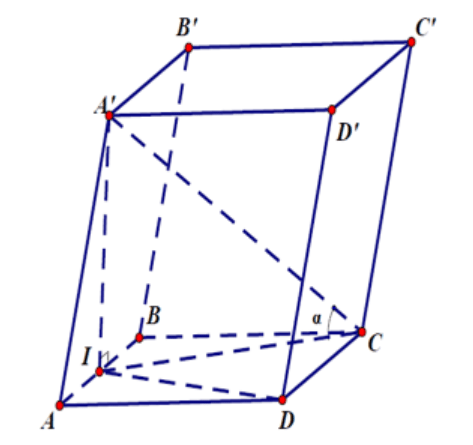
- A. $\frac{1}{6}$a$^{3}$
- B. $\frac{\sqrt{3}}{6}$a$^{3}$
- C. $\frac{\sqrt{3}}{3}$a$^{3}$
-
D. $\frac{1}{3}$a$^{3}$
Câu 12: Cho hình lăng trụ tam giác ABC.A’B’C’có BB’ = a góc giữa đường thẳng BB’ và mặt phẳng (ABC) bằng 60$^{o}$, tam giác ABC vuông tại C và góc (BAC) =60$^{o}$. Hình chiếu vuông góc của điểm B’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Thể tích khối tứ diện A’ABC là
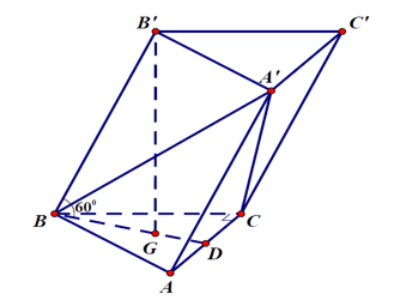
- A. $\frac{3}{208}$a$^{3}$
-
B. $\frac{9}{208}$a$^{3}$
- C. $\frac{1}{108}$a$^{3}$
- D. $\frac{9}{108}$a$^{3}$
Câu 13: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc 45$^{o}$. Tính thể tích khối lăng trụ.
- A. $\frac{3}{32}$a$^{3}$
- B. $\frac{3}{4}$a$^{3}$
- C. $\frac{3}{8}$a$^{3}$
-
D. $\frac{3}{16}$a$^{3}$
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA = a, SB=a$\sqrt{3}$ và mặt phẳng (SAB) vuông góc với mặt phẳng đát. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC. Tính theo a thể tích khối chóp S.ABCD.
-
A. $\frac{\sqrt{3}}{3}$a$^{3}$
- B. $\frac{1}{3}$a$^{3}$
- C. $\frac{\sqrt{2}}{2}$a$^{3}$
- D. $\frac{\sqrt{2}}{3}$a$^{3}$
Câu 15: Thể tích của một khối chóp thay đổi như thế nào nếu tăng diện tích đáy lên 2 lần và giảm độ dài đường cao xuống 2 lần?
-
A. Thể tích không thay đổi
- B. Thể tích giảm xuống 2 lần
- C. Thể tích tăng lên 2 lần
- D. Thể tích tăng lên 4 lần
Câu 16: Cho khối chóp S.ABCD có ABCD là hình vuông cạnh bằng 2a ; SAD là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm của CD. Góc giữa hai mặt phẳng (SBM) và (ABCD) bằng 60$^{o}$. Tính thể tích khối chóp S.ABCD.
- A. $\frac{6}{\sqrt{3}}$a$^{3}$
-
B. $\frac{4\sqrt{15}}{5}a$^{3}$
- C. $\frac{2\sqrt{15}}{5}$a$^{3}$
- D. a$\sqrt{3}$a$^{3}$
Câu 17: Cho khối chóp S.ABC. Lấy A’, B’ lần lượt thuộc SA, SB sao cho 2SA’ = 3A’A, 3SB’ = B’B. Tỉ số thể tích giữa hai khối chóp S.A’B’C và S.ABC là:
-
A. $\frac{3}{20}$
- B. $\frac{2}{15}$
- C. $\frac{1}{6}$
- D. $\frac{3}{10}$
Câu 18: Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau. BA = 3a, BC = BD = 2a. Gọi M, B lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM.
- A. 8a$^{3}$
- B. $\frac{2}{3}$a$^{3}$
- C. a$^{3}$
-
D. $\frac{3}{2}$a$^{3}$
Câu 19: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là trung điểm của SB và G là trọng tâm của tam giác SBc. Gọi V, V’ lần lượt là thể tích các khối chóp M.ABC và G.ABD. Tính tỉ số V/V’
-
A. $\frac{3}{2}$
- B. $\frac{4}{3}$
- C. $\frac{5}{3}$
- D.2
Câu 20: Cho khối chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N theo thứ tự là trung điểm của SA, SB. Tính tỉ số thể tích: $\frac{VS.CDMN}{VS.CDAB}$?
- A. $\frac{1}{2}$
-
B. $\frac{3}{8}$
- C. $\frac{5}{8}$
- D. 4
Câu 21: Cho tứ diện ABCD có thể tích bằng V. Gọi B’, D’ lần lượt là trung điểm của các cạnh AB và AD. Mặt phẳng (CB’D’) chia khối tứ diện thành hai phần. Tính tỉ số thể tích hai phần đó.
- A. $\frac{1}{6}$
- B. $\frac{1}{9}$
- C. $\frac{1}{12}$
-
D. $\frac{1}{3}$
Câu 22: Cho hình chóp S.ACBD có đáy là hình thoi cạnh a, BAD= 120${o}$. Hình chiếu vuông góc của S trên đáy là điểm H thuộc cạnh AB thỏa mãn HB= 3HA. Góc giữa cạnh SC và đáy bằng 60$^{o}$. Tính thể tích khối chóp S.ABCD?
- A. $\frac{3\sqrt{13}}{8}$a$^{3}$
- B. $\frac{5}{8}a$^{3}$
- C. $\frac{5}{24}a$^{3}$
-
D. $\frac{\sqrt{13}}{8}$a$^{3}$
Câu 23: Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc; AB= 6a, AC= 7a và AD= 4a. GỌi M, N, P lần lượt là trung điểm của các cạnh BC, CD, DB. Tính thể tích của tứ diện AMNP.
- A. $\frac{7}{2}$a$^{3}$
- B. $\frac{28}{3}$a$^{3}$
-
C. 7a$^{3}$
- D. 14a$^{3}$
Câu 24: Cho hình chóp S.ABCD có đáy là tam giác vuông cân tại B, AC= a$\sqrt{2}$, AS= a, SA vuông góc với đáy. Gọi G là trọng tâm của tam giác SBC. Mặt phẳng đi qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính thể tích khối chóp S.AMN?
- A. $\frac{4}{27}$a$^{3}$
-
B. $\frac{2}{27}$a$^{3}$
- C. $\frac{2}{9}$a$^{3}$
- D. $\frac{4}{9}$a$^{3}$
Câu 25: Cho hình chóp S.ABC có đáy là tam giác vuông tại C, BAC= 60$^{o}$, SB= a, góc giữa SB và đáy bằng 60$^{o}$. Hình chiếu vuông góc của S trên đáy là trọng tâm của tam giác ABC. Tính thể tích khối chóp S. ABC.
- A. $\frac{9}{104}$a$^{3}$
- B. $\frac{27}{104}$a$^{3}$
-
C. $\frac{9}{208}$a$^{3}$
- D. $\frac{27}{208}$a$^{3}$